Exam 11: Hypothesis Tests and Estimation for Population Variances
Exam 1: The Where, Why, and How of Data Collection167 Questions
Exam 2: Graphs, Charts and Tablesdescribing Your Data138 Questions
Exam 3: Describing Data Using Numerical Measures138 Questions
Exam 4: Introduction to Probability125 Questions
Exam 5: Discrete Probability Distributions161 Questions
Exam 6: Introduction to Continuous Probability Distributions122 Questions
Exam 7: Introduction to Sampling Distributions136 Questions
Exam 8: Estimating Single Population Parameters174 Questions
Exam 9: Introduction to Hypothesis Testing183 Questions
Exam 10: Estimation and Hypothesis Testing for Two Population Parameters121 Questions
Exam 11: Hypothesis Tests and Estimation for Population Variances69 Questions
Exam 12: Analysis of Variance162 Questions
Exam 13: Goodness-Of-Fit Tests and Contingency Analysis105 Questions
Exam 14: Introduction to Linear Regression and Correlation Analysis139 Questions
Exam 15: Multiple Regression Analysis and Model Building148 Questions
Exam 16: Analyzing and Forecasting Time-Series Data131 Questions
Exam 17: Introduction to Nonparametric Statistics103 Questions
Exam 18: Introducing Business Analytics48 Questions
Exam 19: Introduction to Decision Analysis48 Questions
Exam 20: Introduction to Quality and Statistical Process Control42 Questions
Select questions type
One of the key quality characteristics in many service environments is that the variation in service time be reasonably small. Recently, a major amusement park company initiated a new line system at one of its parks. It then wished to compare this new system with the old system in place at a comparable park in another state. At issue is whether the standard deviation in waiting time is less under the new line system than under the old line system. The following information was collected:  Assuming that it wishes to conduct the test using a 0.05 level of significance, the null hypothesis should be rejected since the test statistic exceeds the F-critical value from the F-distribution table.
Assuming that it wishes to conduct the test using a 0.05 level of significance, the null hypothesis should be rejected since the test statistic exceeds the F-critical value from the F-distribution table.
(True/False)
4.9/5  (37)
(37)
When conducting a one-tailed hypothesis test of a population variance using a sample size of n = 24 and a 0.10 level of significance, the critical value is:
(Multiple Choice)
4.8/5  (43)
(43)
A manufacturer of industrial plywood has a contract to supply a boat maker with a large amount of plywood. One of the specifications calls for the standard deviation in thickness to not exceed .03 inch. A sample of n = 30 sheets was sampled randomly from a recent production run. The mean thickness was right at the 3/4 inch target thickness and the sample standard deviation was .05 inch. Testing at the 0.05 level of significance, which of the following is true?
(Multiple Choice)
4.7/5  (31)
(31)
The U.S. Golf Association provides a number of services for its members. One of these is the evaluation of golf equipment to make sure that the equipment satisfies the rules of golf. For example, they regularly test the golf balls made by the various companies that sell balls in the United States. Recently, they undertook a study of two brands of golf balls with the objective to see whether there is a difference in the mean distance that the two golf ball brands will fly off the tee. To conduct the test, the U.S.G.A. uses a robot named "Iron Byron," which swings the club at the same speed and with the same swing pattern each time it is used. The following data reflect sample data for a random sample of balls of each brand.  Given this information, what is the test statistic for testing whether the two population variances are equal?
Given this information, what is the test statistic for testing whether the two population variances are equal?
(Multiple Choice)
4.9/5  (38)
(38)
One of the key quality characteristics in many service environments is that the variation in service time be reasonably small. Recently, a major amusement park company initiated a new line system at one of its parks. It then wished to compare this new system with the old system in place at a comparable park in another state. At issue is whether the standard deviation in waiting time is less under the new line system than under the old line system. The following information was collected:  Assuming that it wishes to conduct the test using a 0.05 level of significance, the correct null and alternative hypotheses would be:
Assuming that it wishes to conduct the test using a 0.05 level of significance, the correct null and alternative hypotheses would be: 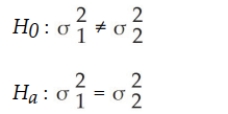
(True/False)
4.8/5  (39)
(39)
A contract calls for the strength of a steel rod to stand up to pressure of 200 lbs per square inch on average. The contract also requires that the variability in strength for individual steel rods be no more than 5 pounds per square inch. If a random sample of n = 15 rods is selected and the sample standard deviation is 6.7 pounds, the test statistic is approximately χ2 = 25.138.
(True/False)
4.8/5  (39)
(39)
If a hypothesis test for a single population variance is to be conducted using a significance level of 0.10, a sample size of n = 16, and the test is a one-tailed upper-tail test, the critical value is:
(Multiple Choice)
4.8/5  (30)
(30)
A potato chip manufacturer has found that in the past the standard deviation of bag weight has been 0.2 ounce. They want to test whether the standard deviation has changed. The null hypothesis is:
(Multiple Choice)
4.9/5  (35)
(35)
If a one-tailed F-test is employed when testing a null hypothesis about two population variances, the test statistic is an F-value formed by taking the ratio of the two sample variances so that the sample variance predicted to be larger is placed in the numerator.
(True/False)
4.8/5  (46)
(46)
A frozen food company that makes burritos currently has employees making burritos by hand. It is considering purchasing equipment to automate the process and wants to determine if the automated process would result in lower variability of burrito weights. It takes a random sample from each process as shown below.  In conducting the hypothesis test, the test statistic is F = 1.375.
In conducting the hypothesis test, the test statistic is F = 1.375.
(True/False)
4.7/5  (37)
(37)
In a test for determining whether two population variances are the same or different, the larger the sample sizes from the two populations, the lower will be the chance of making a Type I statistical error.
(True/False)
4.8/5  (37)
(37)
Similar to the chi-square distribution, all F-tests are one-tailed tests.
(True/False)
4.9/5  (34)
(34)
To test the following hypotheses at the 0.05 level of significance, using a sample size of n = 15. 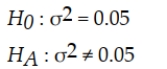 What is the upper tail critical value?
What is the upper tail critical value?
(Multiple Choice)
4.7/5  (33)
(33)
The variance in the diameter of a bolt should not exceed 0.500 mm. A random sample of n = 12 bolts showed a sample variance of 0.505 mm. The test statistic is χ2 = 11.11.
(True/False)
4.8/5  (24)
(24)
A first step in testing whether two populations have the same mean value using the t-distribution is to use the chi-square distribution to test whether the populations have equal variances.
(True/False)
4.9/5  (23)
(23)
One of the major automobile makers has developed two new engines. At question is whether the two engines have the same variability with respect to miles per gallon. To test this using a 0.10 level of significance, the following information is available:  Based on this situation and the information provided, the null hypothesis cannot be rejected and it is possible that the two engines produce the same variation in mpg.
Based on this situation and the information provided, the null hypothesis cannot be rejected and it is possible that the two engines produce the same variation in mpg.
(True/False)
4.9/5  (40)
(40)
The F test statistic for testing whether the variances of two populations are the same is always positive.
(True/False)
5.0/5  (32)
(32)
In performing a one-tailed test for the difference between two population variances, which of the following statements is true?
(Multiple Choice)
4.7/5  (34)
(34)
The central location and shape of the chi-square distribution depend only on the population variance.
(True/False)
4.8/5  (29)
(29)
Showing 41 - 60 of 69
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)