Exam 1: A: the Foundations: Logic and Proofs

Using c for "it is cold" and w for "it is windy," write "To be windy it is necessary that it be cold" in symbols.

write the negation of the statement. (Don't write "It is not true that . . . .") -It is Thursday and it is cold.

Give a direct proof of the following: "If x is an odd integer and y is an even integer, then x + y is odd."

Explain why an argument of the following form is not valid:

Show that the premises "Jean is a student in my class" and "No student in my class is from England" imply the conclusion "Jean is not from England."

suppose the variable x represents students, F(x) means "x is a freshman," and M(x) means "x is a math major." Match the statement in symbols with one of the English statements in this list: 1. Some freshmen are math majors. 2. Every math major is a freshman. 3. No math major is a freshman. - $\neg \exists x ( M ( x ) \wedge \neg F ( x ) )$

P(m, n) means "m ≤ n," where the universe of discourse for m and n is the set of nonnegative integers. What is the truth value of the statement? - $\exists n \forall m P ( m , n )$

suppose the variable x represents students, y represents courses, and T(x, y) means "x is taking y." Match the English statement with all its equivalent symbolic statements in this list: 1. \existsx\forallyT(x,y) 2. \existsy\forallxT(x,y) 3. \forallx\existsyT(x,y) 4. \neg\existsx\existsyT(x,y) 5. \existsx\forally\negT(x,y) 6. \forally\existsxT(x,y) 7. \existsy\forallx\negT(x,y) 8. \neg\forallx\existsyT(x,y) 9. \neg\existsy\forallxT(x,y) 10. \neg\forallx\existsy\negT(x,y) 11. \neg\forallx\neg\forally\negT(x,y) 12. \forallx\existsy\negT(x,y) -Some courses are being taken by no students.

suppose the variable x represents students, F(x) means "x is a freshman," and M(x) means "x is a math major." Match the statement in symbols with one of the English statements in this list: 1. Some freshmen are math majors. 2. Every math major is a freshman. 3. No math major is a freshman. - $\forall x ( \neg ( M ( x ) \wedge \neg F ( x ) ) )$

Write the contrapositive, converse, and inverse of the following: You sleep late if it is Saturday.

Find the output of the combinatorial circuits -

suppose the variable x represents students and y represents courses, and: 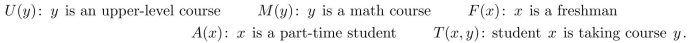Write the statement using these predicates and any needed quantifiers. -Every part-time freshman is taking some upper-level course.

In 110-112 suppose the variable x represents people, and $F ( x ) : x \text { is friendly } T ( x ) : x \text { is tall } A ( x ) : x \text { is angry. }$ Write the statement using these predicates and any needed quantifiers. -All tall people are friendly.

Prove that ¬p → ¬q and its inverse are not logically equivalent.

What is the negation of the propositions -4.5 + 2.5 = 6

Find a proposition with three variables $p , q$ , and $\gamma$ that is true when $p$ and $\gamma$ are true and $q$ is false, and false otherwise.

suppose that Q(x) is "x + 1 = 2x," where x is a real number. Find the truth value of the statement. - $\forall x Q ( x )$

write the statement in the form "If . . . , then . . . ." -To get a good grade it is necessary that you study.

write the statement in the form "If . . . , then . . . ." -You need to be registered in order to check out library books.

Find a proposition with three variables $p , q$ , and $\gamma$ , that is true when at most one of the three variables is true, and false otherwise.