Exam 1: A: the Foundations: Logic and Proofs
Exam 1: The Foundations: Logic and Proofs18 Questions
Exam 1: A: the Foundations: Logic and Proofs201 Questions
Exam 2: Basic Structures: Sets, Functions, Sequences, Sums, Matrices5 Questions
Exam 2: A: Basic Structures: Sets, Functions, Sequences, Sums, Matrices210 Questions
Exam 3: Algorithms8 Questions
Exam 3: A: Algorithms54 Questions
Exam 4: Number Theory and Cryptography10 Questions
Exam 4: A: Number Theory and Cryptography149 Questions
Exam 5: Induction and Recursion10 Questions
Exam 5: A: Induction and Recursion51 Questions
Exam 6: Counting14 Questions
Exam 6: A: Counting155 Questions
Exam 7: Discrete Probability9 Questions
Exam 7: A: Discrete Probability50 Questions
Exam 8: Advanced Counting Techniques16 Questions
Exam 8: A: Advanced Counting Techniques124 Questions
Exam 9: Relations13 Questions
Exam 9: A: Relations72 Questions
Exam 10: Graphs14 Questions
Exam 10: A: Graphs131 Questions
Exam 11: Trees13 Questions
Exam 11: A: Trees94 Questions
Exam 12: Boolean Algebra11 Questions
Exam 12: A: Boolean Algebra67 Questions
Exam 13: Modeling Computation14 Questions
Exam 13: A: Modeling Computation67 Questions
Exam 14: Mathematics Problem Set: Set Theory, Number Theory, Combinatorics, and Boolean Algebra29 Questions
Select questions type
suppose the variable x represents students, F(x) means "x is a freshman," and M(x) means "x is a math major." Match the statement in symbols with one of the English statements in this list:
1. Some freshmen are math majors.
2. Every math major is a freshman.
3. No math major is a freshman.
-
(Short Answer)
4.8/5  (35)
(35)
express the negation of the statement in terms of quantifiers without using the negation symbol.
-
(Short Answer)
4.9/5  (26)
(26)
suppose the variables x and y represent real numbers, and Write the statement using these predicates and any needed quantifiers.
-Every integer is even.
(Short Answer)
4.7/5  (30)
(30)
(a) Find a proposition with the truth table at the right.
(b) Find a proposition using only , and the connective that has this truth table.
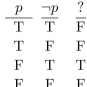
(Short Answer)
4.8/5  (34)
(34)
suppose the variable x represents students, y represents courses, and T(x, y) means "x is taking y." Match the English statement with all its equivalent symbolic statements in this list: 1. \existsx\forallyT(x,y) 2. \existsy\forallxT(x,y) 3. \forallx\existsyT(x,y) 4. \neg\existsx\existsyT(x,y) 5. \existsx\forally\negT(x,y) 6. \forally\existsxT(x,y) 7. \existsy\forallx\negT(x,y) 8. \neg\forallx\existsyT(x,y) 9. \neg\existsy\forallxT(x,y) 10. \neg\forallx\existsy\negT(x,y) 11. \neg\forallx\neg\forally\negT(x,y) 12. \forallx\existsy\negT(x,y)
-There is a course that no students are taking.
(Short Answer)
4.9/5  (42)
(42)
suppose P(x, y) is a predicate and the universe for the variables x and y is {1, 2, 3}. Suppose
P(1, 3), P(2, 1), P(2, 2), P(2, 3), P(3, 1), P(3, 2) are true, and P(x, y) is false otherwise. Determine whether the following statements are true.
-
(True/False)
4.9/5  (37)
(37)
determine whether the proposition is TRUE or FALSE.
-1 + 1 = 3 if and only if 2 + 2 = 3.
(True/False)
4.9/5  (29)
(29)
suppose the variable x represents people, and Write the statement in good English. Do not use variables in your answer.
-
(Short Answer)
4.9/5  (40)
(40)
Consider the following theorem: "if x and y are odd integers, then x + y is even." Give a proof by contradiction of this theorem.
(Essay)
4.8/5  (30)
(30)
assume that the universe for x is all people and the universe for y is the set of all movies. Write the
statement in good English, using the predicates Do not use variables in your answer.
-
(Short Answer)
4.9/5  (38)
(38)
assume that the universe for x is all people and the universe for y is the set of all movies. Write the
English statement using the following predicates and any needed quantifiers:
-Ben has never seen a movie that won an award.
(Short Answer)
4.9/5  (25)
(25)
suppose the variable x represents students and y represents courses, and: is a math course is a freshman is a full-time student is taking . Write the statement in good English without using variables in your answers.
-
(Short Answer)
4.7/5  (26)
(26)
P(x, y) means "x + 2y = xy," where x and y are integers. Determine the truth value of the statement.
-P(1, −1)
(True/False)
4.9/5  (33)
(33)
Find a proposition with three variables , and that is never true.
(Short Answer)
4.7/5  (31)
(31)
assume that the universe for x is all people and the universe for y is the set of all movies. Write the
English statement using the following predicates and any needed quantifiers:
-No comedy won an award.
(Short Answer)
4.8/5  (33)
(33)
A student is asked to give the negation of "all bananas are ripe."
(a) The student responds "all bananas are not ripe." Explain why the English in the student's response is ambiguous.
(b) Another student says that the negation of the statement is "no bananas are ripe." Explain why this is not correct.
(c) Another student says that the negation of the statement is "some bananas are ripe." Explain why this is not correct.
(d) Give the correct negation.
(Essay)
5.0/5  (33)
(33)
Express r ⊕ d in English, where r is "it is rainy" and d is "it is dry."
(Essay)
4.9/5  (26)
(26)
suppose the variables x and y represent real numbers, and Write the statement in good English without using any variables in your answer.
-
(Short Answer)
4.8/5  (25)
(25)
Consider the following theorem: "if x and y are odd integers, then x + y is even." Give a direct proof of this theorem.
(Essay)
4.9/5  (47)
(47)
Showing 121 - 140 of 201
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)