Exam 1: A: the Foundations: Logic and Proofs

Determine whether $( p \rightarrow q ) \wedge ( \neg p \rightarrow q ) \equiv q$ .

P(m, n) means "m ≤ n," where the universe of discourse for m and n is the set of nonnegative integers. What is the truth value of the statement? - $\forall m \exists n P ( m , n )$

suppose the variable x represents students and the variable y represents courses, and $T ( x , y ) : x \text { is taking } y \quad P ( x , y ) : x \text { passed } y \text {. }$ Write the statement in good English. Do not use variables in your answers. - $\forall x \exists y T ( x , y )$

suppose the variable x represents students, F(x) means "x is a freshman," and M(x) means "x is a math major." Match the statement in symbols with one of the English statements in this list: 1. Some freshmen are math majors. 2. Every math major is a freshman. 3. No math major is a freshman. - $\forall x ( M ( x ) \rightarrow \neg F ( x ) )$

suppose the variable x represents students, y represents courses, and T(x, y) means "x is taking y." Match the English statement with all its equivalent symbolic statements in this list: 1. \existsx\forallyT(x,y) 2. \existsy\forallxT(x,y) 3. \forallx\existsyT(x,y) 4. \neg\existsx\existsyT(x,y) 5. \existsx\forally\negT(x,y) 6. \forally\existsxT(x,y) 7. \existsy\forallx\negT(x,y) 8. \neg\forallx\existsyT(x,y) 9. \neg\existsy\forallxT(x,y) 10. \neg\forallx\existsy\negT(x,y) 11. \neg\forallx\neg\forally\negT(x,y) 12. \forallx\existsy\negT(x,y) -No student is taking all courses.

suppose the variable x represents students and y represents courses, and: 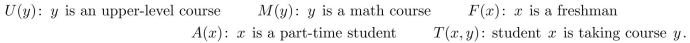Write the statement using these predicates and any needed quantifiers. -There is a part-time student who is not taking any math course.

suppose P(x, y) is a predicate and the universe for the variables x and y is {1, 2, 3}. Suppose P(1, 3), P(2, 1), P(2, 2), P(2, 3), P(3, 1), P(3, 2) are true, and P(x, y) is false otherwise. Determine whether the following statements are true. - $\forall x \exists y P ( x , y )$

Find the output of the combinatorial circuits -

write the negation of the statement in good English. Don't write "It is not true that . . . ." -Roses are red and violets are blue.

suppose the variable x represents students, y represents courses, and T(x, y) means "x is taking y." Match the English statement with all its equivalent symbolic statements in this list: 1. \existsx\forallyT(x,y) 2. \existsy\forallxT(x,y) 3. \forallx\existsyT(x,y) 4. \neg\existsx\existsyT(x,y) 5. \existsx\forally\negT(x,y) 6. \forally\existsxT(x,y) 7. \existsy\forallx\negT(x,y) 8. \neg\forallx\existsyT(x,y) 9. \neg\existsy\forallxT(x,y) 10. \neg\forallx\existsy\negT(x,y) 11. \neg\forallx\neg\forally\negT(x,y) 12. \forallx\existsy\negT(x,y) -No course is being taken by all students.

Construct a combinatorial circuit using inverters, OR gates, and AND gates, that produces the outputs from input bits p, q and r. - $( ( p \vee \neg q ) \wedge r ) \wedge ( ( \neg p \wedge \neg q ) \vee r )$

suppose the variable x represents students and y represents courses, and: $U ( y ) : y$ is an upper-level course $\quad M ( y ) : y$ is a math course $\quad F ( x ) : x$ is a freshman $B ( x )$ : $x$ is a full-time student $\quad T ( x , y )$ : student $x$ is taking course $y$ . Write the statement using these predicates and any needed quantifiers. -All students are freshmen.

write the negation of the statement in good English. Don't write "It is not true that . . . ." -No tests are easy.

suppose the variable x represents students, F(x) means "x is a freshman," and M(x) means "x is a math major." Match the statement in symbols with one of the English statements in this list: 1. Some freshmen are math majors. 2. Every math major is a freshman. 3. No math major is a freshman. - $\neg \exists x ( M ( x ) \wedge \neg F ( x ) )$

P(x, y) means "x + 2y = xy," where x and y are integers. Determine the truth value of the statement. -P(0, 0)

P(x, y) means "x + 2y = xy," where x and y are integers. Determine the truth value of the statement. - $\exists x \forall y P ( x , y )$

write the statement in the form "If . . . , then . . . ." -It is hot whenever it is sunny.

assume that the universe for x is all people and the universe for y is the set of all movies. Write the statement in good English, using the predicates $S ( x , y ) : x \text { saw } y \quad L ( x , y ) : x \text { liked } y \text {. }$ Do not use variables in your answer. - $\exists y \forall x L ( x , y )$

write the statement in the form "If . . . , then . . . ." -The team wins if the quarterback can pass.

Using c for "it is cold" and d for "it is dry," write "It is neither cold nor dry" in symbols.