Exam 7: Applications of Definite Integrals
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and
lines about the x-axis.
-
(Multiple Choice)
4.8/5  (23)
(23)
The centroid of a triangle lies at the intersection of the triangle's medians, because it lies one-third of the way from each
side towards the opposite vertex. Use this result to find the centroid of the triangle whose vertices appear as following.
-(0, 0), (4, 0), (2, 8)
(Multiple Choice)
4.8/5  (37)
(37)
Find the volume of the solid generated by revolving the region about the y-axis.
-The region enclosed by
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-A swimming pool has a rectangular base long and wide. The sides are high, and the pool is full of water. How much work will it take to lower the water level 2 feet by pumping the water out over the top of the pool? Assume that the water weighs . Give your answer to the nearest .
(Multiple Choice)
4.9/5  (25)
(25)
Provide an appropriate response.
-The region shown here is to be revolved about the line to generate a solid. Which of the methods (disk, washer, shell) could you use to find the volume of the solid? How many integrals would be required in each cas
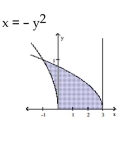
(Essay)
4.9/5  (43)
(43)
A variable force of magnitude moves a body of mass along the -axis from to . The net work done by the force in moving the body from to is , where and are the body's velocities at and . Knowing that the work done by the force equals the change in the body's kinetic energy, solve the problem.
-A 2-oz tennis ball was served at about ( ). How much work was done on the ball to make it go this fast? (To find the ball's mass from its weight, express the weight in pounds and divide by , the acceleration of gravity.)
(Multiple Choice)
4.8/5  (31)
(31)
Find the center of mass of a thin plate of constant density covering the given region.
-The region cut from the first quadrant by the circle
(Multiple Choice)
4.8/5  (35)
(35)
Use the shell method to find the volume of the solid generated by revolving the shaded region about the indicated axis.
-About the -axis
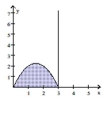
(Multiple Choice)
4.9/5  (31)
(31)
Find the volume of the solid generated by revolving the region about the given line.
-The region bounded above by the line , below by the curve , on the left by the line , and on the right by the line , about the line
(Multiple Choice)
4.7/5  (32)
(32)
The centroid of a triangle lies at the intersection of the triangle's medians, because it lies one-third of the way from each
side towards the opposite vertex. Use this result to find the centroid of the triangle whose vertices appear as following.
-(-9, 0), (9, 0), (0, 2)
(Multiple Choice)
4.8/5  (36)
(36)
Find the volume of the solid generated by revolving the shaded region about the given axis.
-About the -axis
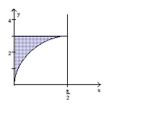
(Multiple Choice)
4.8/5  (36)
(36)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and lines about the y-axis.
-
(Multiple Choice)
4.7/5  (30)
(30)
Find the volume of the solid generated by revolving the region about the given axis. Use the shell or washer method.
-The region bounded by and about the line
(Multiple Choice)
4.7/5  (32)
(32)
Solve the problem.
-A dome is in the form of a partial sphere, with a hemisphere of radius 10 feet on top and the remaining part of the sphere extending 5 feet to the ground from the center of the sphere. Find the surface area of the dome to the nearest square foot.
(Multiple Choice)
4.7/5  (32)
(32)
Find the volume of the solid generated by revolving the region bounded by the given lines and curves about the x-axis.
-
(Multiple Choice)
4.9/5  (37)
(37)
Find the volume of the described solid.
-The base of a solid is the region between the curve and the -axis from to . The cross sections perpendicular to the -axis are squares with bases running from the -axis to the curve.
(Multiple Choice)
4.8/5  (39)
(39)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and lines about the y-axis.
-
(Multiple Choice)
4.8/5  (35)
(35)
Find the volume of the solid generated by revolving the region about the y-axis.
-The region enclosed by
(Multiple Choice)
4.9/5  (37)
(37)
Showing 21 - 40 of 258
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)