Exam 7: Applications of Definite Integrals
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Find the volume of the solid generated by revolving the region about the given axis. Use the shell or washer method.
-The region in the first quadrant bounded by and the -axis about the line
Free
(Multiple Choice)
4.8/5  (35)
(35)
Correct Answer:
D
Solve.
-Find the volume of the torus generated by revolving the circle about the -axis.
Free
(Multiple Choice)
4.8/5  (38)
(38)
Correct Answer:
D
Use your grapher to find the surface's area numerically.
-
Free
(Multiple Choice)
5.0/5  (37)
(37)
Correct Answer:
C
Find the center of mass of a thin plate of constant density covering the given region.
-The region enclosed by the parabolas and
(Multiple Choice)
4.9/5  (26)
(26)
Use the shell method to find the volume of the solid generated by revolving the shaded region about the indicated line.
-About the line
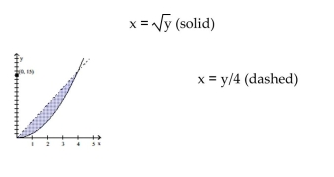
(Multiple Choice)
4.8/5  (30)
(30)
Find the volume of the solid generated by revolving the shaded region about the given axis.
-About the -axis
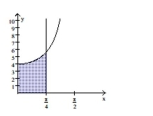
(Multiple Choice)
4.8/5  (36)
(36)
Find the volume of the solid generated by revolving the region bounded by the given lines and curves about the x-axis.
-
(Multiple Choice)
4.9/5  (34)
(34)
Use the shell method to find the volume of the solid generated by revolving the shaded region about the indicated axis.
-About the -axis
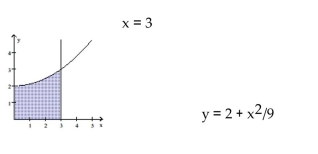
(Multiple Choice)
4.8/5  (41)
(41)
Find the volume of the solid generated by revolving the region bounded by the given lines and curves about the x-axis.
-
(Multiple Choice)
4.8/5  (43)
(43)
Solve the problem.
-A water tank is formed by revolving the curve about the -axis. Find the volume of water in the tank as a function of the water depth, .
(Multiple Choice)
4.9/5  (32)
(32)
Solve the problem.
-A construction crane lifts a 100-lb bucket originally containing 130 lb of sand at a constant rate. The sand leaks out at a constant rate so that there is only 65 lb of sand left when the crane reaches a height of 60 feet. How
Much work is done by the crane?
(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-Find a curve through the point whose length integral, , is .
(Multiple Choice)
4.9/5  (27)
(27)
Find the volume of the solid generated by revolving the shaded region about the given axis.
-About the -axis
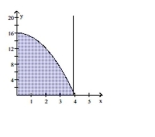
(Multiple Choice)
4.7/5  (34)
(34)
Find the volume of the solid generated by revolving the region about the y-axis.
-The region in the first quadrant bounded on the left by the circle , on the right by the line , and above by the line
(Multiple Choice)
4.8/5  (33)
(33)
Provide an appropriate response.
-The region shown here is to be revolved about the -axis to generate a solid. Which of the methods (disk, washe shell) could you use to find the volume of the solid? How many integrals would be required in each case?
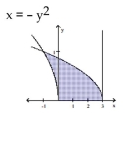
(Essay)
4.8/5  (38)
(38)
Solve the problem.
-A conical tank is resting on its apex. The height of the tank is , and the radius of its top is . The tank is full of gasoline weighing . How much work will it take to pump the gasoline to a level above the cone's top? Give your answer to the nearest ' .
(Multiple Choice)
4.8/5  (40)
(40)
A variable force of magnitude moves a body of mass along the -axis from to . The net work done by the force in moving the body from to is , where and are the body's velocities at and . Knowing that the work done by the force equals the change in the body's kinetic energy, solve the problem.
-How many foot-pounds of work does it take to throw a baseball 20 mph? A baseball weighs 5 oz, or 0.3125 lb.
(Multiple Choice)
4.8/5  (34)
(34)
Find the center of mass of a thin plate of constant density covering the given region.
-The region bounded by the -axis and the curve
(Multiple Choice)
4.9/5  (45)
(45)
Showing 1 - 20 of 258
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)