Exam 5: Applications of Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Provide an appropriate response.
-Decide if the statement is true or false. If false, explain.
The points and lie on the graph of . Therefore, the Mean Value Theorem says that there exists some value on for which
Free
(True/False)
4.8/5  (33)
(33)
Correct Answer:
False
Estimate the limit by graphing the function for an appropriate domain. Confirm your estimate by using L'Hopital's rule.
Show each step of your calculation.
-Find the error in the following incorrect application of L'Hôpital's Rule.
Free
(Essay)
4.7/5  (33)
(33)
Correct Answer:
L'Hopital's Rule cannot be applied to because it corresponds to which is not an indeterminate form.
Find an antiderivative of the given function.
-
Free
(Multiple Choice)
4.7/5  (30)
(30)
Correct Answer:
B
Solve the problem.
-For , sketch a curve that has and . Can anything be said about the concavity of such a curve? Give reasons for your answer.
(Essay)
4.8/5  (37)
(37)
Answer the problem.
-Use the following function and a graphing calculator to answer the questions.
a). Plot the function over the interval to see its general behavior there. Sketch the graph below.
![Answer the problem. -Use the following function and a graphing calculator to answer the questions. f ( x ) = \sqrt { 3 x } + 0.9 \sin x , [ 0,2 \pi ] a). Plot the function over the interval to see its general behavior there. Sketch the graph below. b). Find the interior points where f = 0 (you may need to use the numerical equation solver to approximate a solution). You may wish to plot f as well. List the points as ordered pairs (x, y). c). Find the interior points where f does not exist. List the points as ordered pairs (x, y). d). Evaluate the function at the endpoints and list these points as ordered pairs (x, y). e). Find the function's absolute extreme values on the interval and identify where they occur.](https://storage.examlex.com/TB6591/11ecd900_97c5_9b33_8f2a_cd7651b8637d_TB6591_11.jpg) b). Find the interior points where f = 0 (you may need to use the numerical equation solver to approximate a solution). You may wish to plot f as well. List the points as ordered pairs (x, y).
c). Find the interior points where f does not exist. List the points as ordered pairs (x, y).
d). Evaluate the function at the endpoints and list these points as ordered pairs (x, y).
e). Find the function's absolute extreme values on the interval and identify where they occur.
b). Find the interior points where f = 0 (you may need to use the numerical equation solver to approximate a solution). You may wish to plot f as well. List the points as ordered pairs (x, y).
c). Find the interior points where f does not exist. List the points as ordered pairs (x, y).
d). Evaluate the function at the endpoints and list these points as ordered pairs (x, y).
e). Find the function's absolute extreme values on the interval and identify where they occur.
(Essay)
4.8/5  (36)
(36)
Solve the problem.
-A particle moves on a coordinate line with acceleration , subject to the conditions that and when . Find the velocity in terms of and the position in terms of .
(Multiple Choice)
4.7/5  (39)
(39)
Answer each question appropriately.
-Suppose the velocity of a body moving along the s-axis is .
Find the body's displacement over the time interval from to given that when .
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-A rocket lifts off the surface of Earth with a constant acceleration of . How fast will the rocket be going minutes later?
(Multiple Choice)
4.8/5  (31)
(31)
Determine whether the function satisfies the hypotheses of the Mean Value Theorem for the given interval.
-
(True/False)
4.8/5  (37)
(37)
Find the open intervals on which the function is increasing and decreasing. Identify the function's local and absolute extreme values, if any, saying where they occur.
-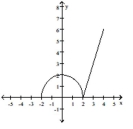
(Multiple Choice)
4.9/5  (44)
(44)
Determine whether the function satisfies the hypotheses of the Mean Value Theorem for the given interval.
-
(True/False)
4.9/5  (34)
(34)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.8/5  (36)
(36)
Graph the function, then find the extreme values of the function on the interval and indicate where they occur.
-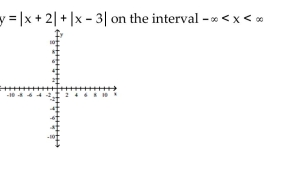
(Multiple Choice)
4.9/5  (36)
(36)
Determine from the graph whether the function has any absolute extreme values on the interval [a, b].
-![Determine from the graph whether the function has any absolute extreme values on the interval [a, b]. -](https://storage.examlex.com/TB6591/11eb49f8_e00f_f04e_b71a_91c0d5e61675_TB6591_00.jpg)
(Multiple Choice)
4.9/5  (47)
(47)
Showing 1 - 20 of 412
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)