Exam 7: Applications of Definite Integrals
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Solve the problem.
-A force of 4 N will stretch a rubber band 5 cm. Assuming Hooke's law applies, how much work is done on the rubber band by a 12 N force?
(Multiple Choice)
4.8/5  (33)
(33)
Find the volume of the solid generated by revolving the region bounded by the given lines and curves about the x-axis.
-
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-The base of a rectangular tank measures by . The tank is tall, and its top is below ground level. The tank is full of water weighing . How much work does it take to empty the tank by pumping the water to ground level? Give your answer to the nearest ' .
(Multiple Choice)
4.9/5  (31)
(31)
Find the center of mass of a thin plate covering the given region with the given density function.
-The region enclosed by the parabolas and , with density
(Multiple Choice)
4.8/5  (21)
(21)
Find the area of the surface generated by revolving the curve about the indicated axis.
-
(Multiple Choice)
4.9/5  (40)
(40)
Provide an appropriate response.
-The region bounded by the lines x = 2, x = 6, y = -2, and y = 1 is revolved about the y-axis to form a solid.
Explain how you could use elementary geometry formulas to verify the volume of this solid.
(Essay)
4.8/5  (38)
(38)
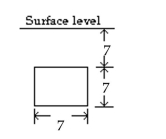
Find the fluid force exerted against the vertically submerged flat surface depicted in the diagram. Assume arbitrary
units, and call the weight-density of the fluid w.
-
(Multiple Choice)
4.8/5  (29)
(29)
Solve the problem.
-A rescue cable attached to a helicopter weighs 2 lb/ft. A 170-lb man grabs the end of the rope and is pulled from the ocean into the helicopter. How much work is done in lifting the man if the helicopter is 50 ft above the
Water?
(Multiple Choice)
4.7/5  (32)
(32)
Find the volume of the solid generated by revolving the shaded region about the given axis.
-About the -axis
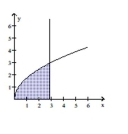
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-A rectangular swimming pool has a parabolic drain plate at the bottom of the pool. The drain plate is shaped like the region between and the line from to . The pool is by and deep. If the drain plate is designed to withstand a fluid force of , how high can the pool be filled without exceeding this limitation?
(Multiple Choice)
4.9/5  (29)
(29)
Find the volume of the solid generated by revolving the region bounded by the given lines and curves about the x-axis.
-
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-A water tank is formed by revolving the curve about the -axis. Water drains from the tank through a small hole in the bottom of the tank. At what constant rate does the water level, , fall? (Use Torricelli's Law: .)
(Multiple Choice)
5.0/5  (34)
(34)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and lines about the y-axis.
-y = 3x, y = 6x, x = 3
(Multiple Choice)
4.9/5  (42)
(42)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves
about the given lines.
- ; revolve about the line
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-It takes a force of 12,000 lb to compress a spring from its free height of 15 in. to its fully compressed height of 10 in. How much work does it take to compress the spring the first inch?
(Multiple Choice)
4.8/5  (33)
(33)
Find the volume of the solid generated by revolving the region bounded by the given lines and curves about the x-axis.
-y = 3x, y = 3, x = 0
(Multiple Choice)
4.8/5  (34)
(34)
Find the volume of the described solid.
-The base of the solid is the disk . The cross sections by planes perpendicular to the -axis between and are isosceles right triangles with one leg in the disk.
(Multiple Choice)
4.8/5  (41)
(41)
Find the area of the surface generated by revolving the curve about the indicated axis.
-
(Multiple Choice)
4.8/5  (27)
(27)
Showing 101 - 120 of 258
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)