Question 1

Provide an appropriate response.
-Determine the point on the plane 6x + 9y + 4z = 15 that is closest to the point (14, 17, 11).

Accepted Answer

A)  (2, -1, 3) 
B)  (2, 1, -3) 
C)  (-2, -1, -3) 
D)  (-2, 1, -3) 
A)  (2, -1, 3) 
B)  (2, 1, -3) 
C)  (-2, -1, -3) 
D)  (-2, 1, -3) A

Question 2

Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-$$f ( x , y ) = \frac { 10 y } { \sqrt { 4 x ^ { 2 } + 6 y ^ { 2 } } }$$

Accepted Answer

Answers will vary. One possibility is Path 1: x = t, y = t ; Path 2: x = 0, y = t

Question 3

Find the linearization of the function at the given point.
-f(x, y, z) = 8xy + 4yz + 8zx at (1, 1, 1)

Accepted Answer

A)  L(x, y, z) = 8x + 4y + 8z - 20 
B)  L(x, y, z) = 16x + 12y + 12z - 20 
C)  L(x, y, z) = 16x + 12y + 12z - 40 
D)  L(x, y, z) = 8x + 4y + 8z - 40 
A)  L(x, y, z) = 8x + 4y + 8z - 20 
B)  L(x, y, z) = 16x + 12y + 12z - 20 
C)  L(x, y, z) = 16x + 12y + 12z - 40 
D)  L(x, y, z) = 8x + 4y + 8z - 40 B

Question 4

Find an upper bound for the magnitude |E| of the error in the approximation f(x, y) ≈ L(x, y) at the given point over the
given region R.
-$$f ( x , y ) = 9 x ^ { 2 } y ^ { 3 } \text { at } ( 2,1 ) ; R : | x - 2 | \leq 0.2 , | y - 1 | \leq 0.2$$

Accepted Answer

A)  $| E | \leq 13.68576$ 
B)  $| \mathrm { E } | \leq 19.65492$ 
C)  $| \mathrm { E } | \leq 25.09056$ 
D)  $| \mathrm { E } | \leq 19.38816$ 
A)  $| E | \leq 13.68576$ 
B)  $| \mathrm { E } | \leq 19.65492$ 
C)  $| \mathrm { E } | \leq 25.09056$ 
D)  $| \mathrm { E } | \leq 19.38816$

Question 5

Solve the problem.
-$\text { Find the equation for the tangent plane to the surface } z = \ln \left( 6 x ^ { 2 } + 7 y ^ { 2 } + 1 \right) \text { at the point } ( 0,0,0 ) \text {. }$

Accepted Answer

A)  x + y = 0 
B)  x - y = 0 
C)  x + y + z = 0 
D)  z = 0 
A)  x + y = 0 
B)  x - y = 0 
C)  x + y + z = 0 
D)  z = 0

Question 6

Solve the problem.
-Find the point on the curve of intersection of the paraboloid $x ^ { 2 } + y ^ { 2 } + 2 z = 4$ and the plane $x - y + 2 z = 0$ that is farthest from the origin.

Accepted Answer

A)  (-2, 2, 2) 
B)  (2, -2, -2) 
C)  (2, -2, 2) 
D)  (-2, -2, 2) 
A)  (-2, 2, 2) 
B)  (2, -2, -2) 
C)  (2, -2, 2) 
D)  (-2, -2, 2)

Question 7

Answer the question.
-Consider a function $\mathrm { f } ( \mathrm { x } , \mathrm { y } , \mathrm { z } )$, where the independent variables are constrained to lie on the curve $\overrightarrow { \mathrm { r } } ( \mathrm { t } ) = \mathrm { x } ( \mathrm { t } ) \mathrm { i } +$ $y ( t ) j + z ( t ) k$. What mathematical fact forms the basis for the method of Lagrange multipliers?

Accepted Answer

A)  $\mathrm { f }$ approaches a local extremum as $\lambda \rightarrow 0$. 
B) ${\nabla} f \cdot \nabla g=0$ 
C)  $\nabla g = 0$ 
D) ${\nabla} f \cdot \vec{v}=0$ 
A)  $\mathrm { f }$ approaches a local extremum as $\lambda \rightarrow 0$. 
B) ${\nabla} f \cdot \nabla g=0$ 
C)  $\nabla g = 0$ 
D) ${\nabla} f \cdot \vec{v}=0$

Question 8

Find all the local maxima, local minima, and saddle points of the function.
-$$f ( x , y ) = 6 x ^ { 2 } y + 5 x y ^ { 2 }$$

Accepted Answer

A)  $f ( 30,30 ) = 297,000$, local maximum 
B)  $\left\{ \left( \frac { 1 } { 5 } , \frac { 1 } { 6 } \right) = \frac { 61 } { 900 } \right.$, local minimum 
C)  $\mathrm { f } ( 0,0 ) = 0$, saddle point 
D)  $\left\{ \left( \frac { 1 } { 6 } , \frac { 1 } { 5 } \right) = \frac { 1 } { 15 } \right.$, local minimum 
A)  $f ( 30,30 ) = 297,000$, local maximum 
B)  $\left\{ \left( \frac { 1 } { 5 } , \frac { 1 } { 6 } \right) = \frac { 61 } { 900 } \right.$, local minimum 
C)  $\mathrm { f } ( 0,0 ) = 0$, saddle point 
D)  $\left\{ \left( \frac { 1 } { 6 } , \frac { 1 } { 5 } \right) = \frac { 1 } { 15 } \right.$, local minimum

Question 9

Find an upper bound for the magnitude |E| of the error in the approximation f(x, y) ≈ L(x, y) at the given point over the
given region R.
-$$\mathrm { f } ( \mathrm { x } , \mathrm { y } , \mathrm { z } ) = 4 \mathrm { xy } + 8 \mathrm { yz } + 10 \mathrm { zx } \text { at } ( 1,1,1 ) ; \mathrm { R } : | \mathrm { x } - 1 | \leq 0.1 , | \mathrm { y } - 1 | \leq 0.1 , | \mathrm { z } - 1 | \leq 0.1$$

Accepted Answer

A)  $| \mathrm { E } | \leq 0.45$ 
B)  $| \mathrm { E } | \leq 0.42$ 
C)  $| \mathrm { E } | \leq 0.35$ 
D)  $| \mathrm { E } | \leq 0.375$ 
A)  $| \mathrm { E } | \leq 0.45$ 
B)  $| \mathrm { E } | \leq 0.42$ 
C)  $| \mathrm { E } | \leq 0.35$ 
D)  $| \mathrm { E } | \leq 0.375$

Question 10

Find the derivative of the function at P0 in the direction of u.
-$$f ( x , y ) = \tan ^ { - 1 } \frac { - 3 x } { y } , \quad P _ { 0 } ( - 7 , - 8 ) , \quad \mathbf { u } = 12 \mathbf { i } - 5 \mathbf { j }$$

Accepted Answer

A)  $\frac { 393 } { 6565 }$ 
B)  $\frac { 456 } { 6565 }$ 
C)  $\frac { 27 } { 505 }$ 
D)  $\frac { 477 } { 6565 }$ 
A)  $\frac { 393 } { 6565 }$ 
B)  $\frac { 456 } { 6565 }$ 
C)  $\frac { 27 } { 505 }$ 
D)  $\frac { 477 } { 6565 }$

Question 11

Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-$\text { Define } f ( 0,0 ) \text { in a way that extends } f ( x , y ) = \frac { x ^ { 2 } y ^ { 2 } } { x ^ { 2 } + y ^ { 2 } } \text { to be continuous at the origin. }$

Accepted Answer

A)  f(0, 0) = 1 
B)  No definition makes f(x, y) continuous at the origin. 
C)  f(0, 0) = 0 
D)  f(0, 0) = 2 
A)  f(0, 0) = 1 
B)  No definition makes f(x, y) continuous at the origin. 
C)  f(0, 0) = 0 
D)  f(0, 0) = 2

Question 12

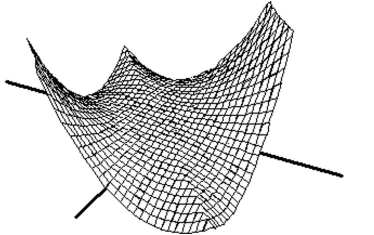
Match the surface show below to the graph of its level curves.
-

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Question 13

Find the linearization of the function at the given point.
-$f ( x , y , z ) = \tan ^ { - 1 } x y z$ at $( 9,9,9 )$

Accepted Answer

A)  $L ( x , y , z ) = \frac { 81 } { 6562 } x + \frac { 81 } { 6562 } y + \frac { 81 } { 6562 } z + \tan ^ { - 1 } 81 - \frac { 243 } { 6562 }$ 
B)  $L ( x , y , z ) = \frac { 81 } { 6562 } x + \frac { 81 } { 6562 } y + \frac { 81 } { 6562 } z + \tan ^ { - 1 } 729 - \frac { 243 } { 6562 }$ 
C)  $L ( x , y , z ) = \frac { 81 } { 531,442 } x + \frac { 81 } { 531,442 } y + \frac { 81 } { 531,442 } z + \tan ^ { - 1 } 729 - \frac { 2187 } { 531,442 }$ 
D)  $\mathrm { L } ( \mathrm { x } , \mathrm { y } , \mathrm { z } ) = \frac { 81 } { 531,442 } \mathrm { x } + \frac { 81 } { 531,442 } \mathrm { y } + \frac { 81 } { 531,442 } \mathrm { z } + \tan ^ { - 1 } 81 - \frac { 2187 } { 531,442 }$ 
A)  $L ( x , y , z ) = \frac { 81 } { 6562 } x + \frac { 81 } { 6562 } y + \frac { 81 } { 6562 } z + \tan ^ { - 1 } 81 - \frac { 243 } { 6562 }$ 
B)  $L ( x , y , z ) = \frac { 81 } { 6562 } x + \frac { 81 } { 6562 } y + \frac { 81 } { 6562 } z + \tan ^ { - 1 } 729 - \frac { 243 } { 6562 }$ 
C)  $L ( x , y , z ) = \frac { 81 } { 531,442 } x + \frac { 81 } { 531,442 } y + \frac { 81 } { 531,442 } z + \tan ^ { - 1 } 729 - \frac { 2187 } { 531,442 }$ 
D)  $\mathrm { L } ( \mathrm { x } , \mathrm { y } , \mathrm { z } ) = \frac { 81 } { 531,442 } \mathrm { x } + \frac { 81 } { 531,442 } \mathrm { y } + \frac { 81 } { 531,442 } \mathrm { z } + \tan ^ { - 1 } 81 - \frac { 2187 } { 531,442 }$

Question 14

Solve the problem.
-The surface area of a hollow cylinder (tube) is given by $S = 2 \pi \left( R _ { 1 } + R _ { 2 } \right) \left( h + R _ { 1 } - R _ { 2 } \right) ,$ where $\mathrm { h }$ is the length of the cylinder and $\mathrm { R } _ { 1 }$ and $\mathrm { R } _ { 2 }$ are the outer and inner radii. If $\mathrm { h } _ { , } \mathrm { R } _ { 1 }$, and $\mathrm { R } _ { 2 }$ are measured to be 10 inches, 3 inches, and 5 inches respectively, and if these measurements are accurate to within $0.1$ inches, estimate the maximum possible error in computing $S$.

Accepted Answer

A)  15.08 
B)  16.96 
C)  11.31 
D)  13.19 
A)  15.08 
B)  16.96 
C)  11.31 
D)  13.19

Question 15

Give an appropriate answer.
-$$f ( x , y ) = \sin ^ { 2 } \left( - 2 x y ^ { 2 } - y \right)$$

Accepted Answer

A)  $\frac { \partial f } { \partial x } = 2 \sin \left( - 2 x y ^ { 2 } - y \right) \cos \left( - 2 x y ^ { 2 } - y \right) ; \frac { \partial f } { \partial y } = ( - 8 x - 2 ) \sin \left( - 2 x y ^ { 2 } - y \right) \cos \left( - 2 x y ^ { 2 } - y \right)$ 
B)  $\frac { \partial f } { \partial x } = 2 \sin \left( - 2 x y ^ { 2 } - y \right) \cos \left( - 2 x y ^ { 2 } - y \right) ; \frac { \partial f } { \partial y } = 2 \sin \left( - 2 x y ^ { 2 } - y \right) \cos \left( - 2 x y ^ { 2 } - y \right)$ 
C)  $\frac { \partial f } { \partial x } = - 4 y ^ { 2 } \sin \left( - 2 x y ^ { 2 } - y \right) \cos \left( - 2 x y ^ { 2 } - y \right) ; \frac { \partial f } { \partial y } = ( - 8 x y - 2 ) \sin \left( - 2 x y ^ { 2 } - y \right) \cos \left( - 2 x y ^ { 2 } - y \right)$ 
D)  $\frac { \partial f } { \partial x } = - 4 y ^ { 2 } \sin \left( - 2 x y ^ { 2 } - y \right) \cos \left( - 2 x y ^ { 2 } - y \right) ; \frac { \partial f } { \partial y } = 2 \sin \left( - 2 x y ^ { 2 } - y \right) \cos \left( - 2 x y ^ { 2 } - y \right)$ 
A)  $\frac { \partial f } { \partial x } = 2 \sin \left( - 2 x y ^ { 2 } - y \right) \cos \left( - 2 x y ^ { 2 } - y \right) ; \frac { \partial f } { \partial y } = ( - 8 x - 2 ) \sin \left( - 2 x y ^ { 2 } - y \right) \cos \left( - 2 x y ^ { 2 } - y \right)$ 
B)  $\frac { \partial f } { \partial x } = 2 \sin \left( - 2 x y ^ { 2 } - y \right) \cos \left( - 2 x y ^ { 2 } - y \right) ; \frac { \partial f } { \partial y } = 2 \sin \left( - 2 x y ^ { 2 } - y \right) \cos \left( - 2 x y ^ { 2 } - y \right)$ 
C)  $\frac { \partial f } { \partial x } = - 4 y ^ { 2 } \sin \left( - 2 x y ^ { 2 } - y \right) \cos \left( - 2 x y ^ { 2 } - y \right) ; \frac { \partial f } { \partial y } = ( - 8 x y - 2 ) \sin \left( - 2 x y ^ { 2 } - y \right) \cos \left( - 2 x y ^ { 2 } - y \right)$ 
D)  $\frac { \partial f } { \partial x } = - 4 y ^ { 2 } \sin \left( - 2 x y ^ { 2 } - y \right) \cos \left( - 2 x y ^ { 2 } - y \right) ; \frac { \partial f } { \partial y } = 2 \sin \left( - 2 x y ^ { 2 } - y \right) \cos \left( - 2 x y ^ { 2 } - y \right)$

Question 16

Solve the problem.
-Find the maximum value of $f ( x , y , z ) = x + 2 y + 3 z$ subject to $x - y + z = 1$ and $x ^ { 2 } + y ^ { 2 } = 1$.

Accepted Answer

A)  $3 + \sqrt { 29 }$ 
B)  $3 - \sqrt { 37 }$ 
C)  $3 - \sqrt { 29 }$ 
D)  $3 + \sqrt { 37 }$ 
A)  $3 + \sqrt { 29 }$ 
B)  $3 - \sqrt { 37 }$ 
C)  $3 - \sqrt { 29 }$ 
D)  $3 + \sqrt { 37 }$

Question 17

Provide an appropriate response.
-Which of the following space regions is (are) closed?
i. The hemispherical region centered at the origin with $z > 0$ and radius $\mathrm { r }$ bounded by $0 \leq \mathrm { r } \leq \mathrm { r } _ { \mathrm { O } }$
ii. The $x y$-plane
iii. The half-space $x > 0$
iv. Space itself

Accepted Answer

A)  ii only 
B)  ii, iii, and iv 
C)  ii and iv 
D)  iv only 
A)  ii only 
B)  ii, iii, and iv 
C)  ii and iv 
D)  iv only

Question 18

Give an appropriate answer.
-$f ( x , y ) = \left( 10 x ^ { 5 } y ^ { 4 } - 5 \right) ^ { 2 }$

Accepted Answer

A)  $\frac { \partial f } { \partial x } = 50 x ^ { 4 } y ^ { 4 } ; \frac { \partial f } { \partial y } = 40 x ^ { 5 } y ^ { 3 }$ 
B)  $\frac { \partial f } { \partial x } = 100 x ^ { 4 } y ^ { 4 } \left( 10 x ^ { 5 } y ^ { 4 } - 5 \right) ; \frac { \partial f } { \partial y } = 80 x ^ { 5 } y ^ { 3 } \left( 10 x ^ { 5 } y ^ { 4 } - 5 \right)$ 
C)  $\frac { \partial f } { \partial x } = 80 x ^ { 5 } y ^ { 3 } \left( 10 x ^ { 5 } y ^ { 4 } - 5 \right) ; \frac { \partial f } { \partial y } = 100 x ^ { 4 } y ^ { 4 } \left( 10 x ^ { 5 } y ^ { 4 } - 5 \right)$ 
D)  $\frac { \partial f } { \partial x } = 2 \left( 10 x ^ { 5 } y ^ { 4 } - 5 \right) ; \frac { \partial f } { \partial y } = 2 \left( 10 x ^ { 5 } y ^ { 4 } - 5 \right)$ 
A)  $\frac { \partial f } { \partial x } = 50 x ^ { 4 } y ^ { 4 } ; \frac { \partial f } { \partial y } = 40 x ^ { 5 } y ^ { 3 }$ 
B)  $\frac { \partial f } { \partial x } = 100 x ^ { 4 } y ^ { 4 } \left( 10 x ^ { 5 } y ^ { 4 } - 5 \right) ; \frac { \partial f } { \partial y } = 80 x ^ { 5 } y ^ { 3 } \left( 10 x ^ { 5 } y ^ { 4 } - 5 \right)$ 
C)  $\frac { \partial f } { \partial x } = 80 x ^ { 5 } y ^ { 3 } \left( 10 x ^ { 5 } y ^ { 4 } - 5 \right) ; \frac { \partial f } { \partial y } = 100 x ^ { 4 } y ^ { 4 } \left( 10 x ^ { 5 } y ^ { 4 } - 5 \right)$ 
D)  $\frac { \partial f } { \partial x } = 2 \left( 10 x ^ { 5 } y ^ { 4 } - 5 \right) ; \frac { \partial f } { \partial y } = 2 \left( 10 x ^ { 5 } y ^ { 4 } - 5 \right)$

Question 19

Solve the problem.
-Maximize $f ( x , y ) = 2 x ^ { 2 } + 10 x y + 9 y ^ { 2 }$ subject to $x + y = 1$ and $x + 4 y = 9$.

Accepted Answer

A)  $\frac { 226 } { 9 }$ 
B)  $- \frac { 58 } { 3 }$ 
C)  $\frac { 26 } { 9 }$ 
D)  $\frac { 142 } { 3 }$ 
A)  $\frac { 226 } { 9 }$ 
B)  $- \frac { 58 } { 3 }$ 
C)  $\frac { 26 } { 9 }$ 
D)  $\frac { 142 } { 3 }$

Question 20

Give an appropriate answer.
-$$f ( x , y ) = \ln \left( \frac { y ^ { 10 } } { x ^ { 9 } } \right)$$

Accepted Answer

A)  $\frac { \partial f } { \partial x } = - \ln \left( \frac { 9 y ^ { 10 } } { x ^ { 10 } } \right) ; \frac { \partial f } { \partial y } = \ln \left( \frac { 10 y ^ { 9 } } { x ^ { 9 } } \right)$ 
B)  $\frac { \partial f } { \partial x } = \frac { 10 } { y } ; \frac { \partial f } { \partial y } = \frac { 9 } { x }$ 
C)  $\frac { \partial f } { \partial x } = - \frac { 9 } { x } ; \frac { \partial f } { \partial y } = \frac { 10 } { y }$ 
D)  $\frac { \partial f } { \partial x } = - \ln \left( \frac { 9 } { x } \right) ; \frac { \partial f } { \partial y } = \ln \left( \frac { 10 } { y } \right)$ 
A)  $\frac { \partial f } { \partial x } = - \ln \left( \frac { 9 y ^ { 10 } } { x ^ { 10 } } \right) ; \frac { \partial f } { \partial y } = \ln \left( \frac { 10 y ^ { 9 } } { x ^ { 9 } } \right)$ 
B)  $\frac { \partial f } { \partial x } = \frac { 10 } { y } ; \frac { \partial f } { \partial y } = \frac { 9 } { x }$ 
C)  $\frac { \partial f } { \partial x } = - \frac { 9 } { x } ; \frac { \partial f } { \partial y } = \frac { 10 } { y }$ 
D)  $\frac { \partial f } { \partial x } = - \ln \left( \frac { 9 } { x } \right) ; \frac { \partial f } { \partial y } = \ln \left( \frac { 10 } { y } \right)$

Provide an appropriate response. -Determine the point on the plane 6x + 9y + 4z = 15 that is closest to the point (14, 17, 11).

Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0). - $f ( x , y ) = \frac { 10 y } { \sqrt { 4 x ^ { 2 } + 6 y ^ { 2 } } }$

Find the linearization of the function at the given point. -f(x, y, z) = 8xy + 4yz + 8zx at (1, 1, 1)

Find an upper bound for the magnitude |E| of the error in the approximation f(x, y) ≈ L(x, y) at the given point over the given region R. - $f ( x , y ) = 9 x ^ { 2 } y ^ { 3 } \text { at } ( 2,1 ) ; R : | x - 2 | \leq 0.2 , | y - 1 | \leq 0.2$

Solve the problem. - $\text { Find the equation for the tangent plane to the surface } z = \ln \left( 6 x ^ { 2 } + 7 y ^ { 2 } + 1 \right) \text { at the point } ( 0,0,0 ) \text {. }$

Solve the problem. -Find the point on the curve of intersection of the paraboloid $x ^ { 2 } + y ^ { 2 } + 2 z = 4$ and the plane $x - y + 2 z = 0$ that is farthest from the origin.

Find all the local maxima, local minima, and saddle points of the function. - $f ( x , y ) = 6 x ^ { 2 } y + 5 x y ^ { 2 }$

Find the derivative of the function at P0 in the direction of u. - $f ( x , y ) = \tan ^ { - 1 } \frac { - 3 x } { y } , \quad P _ { 0 } ( - 7 , - 8 ) , \quad \mathbf { u } = 12 \mathbf { i } - 5 \mathbf { j }$

Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0). - $\text { Define } f ( 0,0 ) \text { in a way that extends } f ( x , y ) = \frac { x ^ { 2 } y ^ { 2 } } { x ^ { 2 } + y ^ { 2 } } \text { to be continuous at the origin. }$

Match the surface show below to the graph of its level curves. -

Find the linearization of the function at the given point. - $f ( x , y , z ) = \tan ^ { - 1 } x y z$ at $( 9,9,9 )$

Give an appropriate answer. - $f ( x , y ) = \sin ^ { 2 } \left( - 2 x y ^ { 2 } - y \right)$

Solve the problem. -Find the maximum value of $f ( x , y , z ) = x + 2 y + 3 z$ subject to $x - y + z = 1$ and $x ^ { 2 } + y ^ { 2 } = 1$ .

Give an appropriate answer. - $f ( x , y ) = \left( 10 x ^ { 5 } y ^ { 4 } - 5 \right) ^ { 2 }$

Solve the problem. -Maximize $f ( x , y ) = 2 x ^ { 2 } + 10 x y + 9 y ^ { 2 }$ subject to $x + y = 1$ and $x + 4 y = 9$ .

Give an appropriate answer. - $f ( x , y ) = \ln \left( \frac { y ^ { 10 } } { x ^ { 9 } } \right)$

Functions

Limits and Continuity

Derivatives

Applications of Derivatives

Integrals

Applications of Definite Integrals

Integrals and Transcendental Functions

Techniques of Integration

First-Order Differential Equations

Infinite Sequences and Series

Parametric Equations and Polar Coordinates

Vectors and the Geometry of Space

Vector-Valued Functions and Motion in Space

Multiple Integrals

Integrals and Vector Fields

Filters

Exam 15: Partial Derivatives