Exam 3: Limits and Continuity
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Use the graph to evaluate the limit.
-
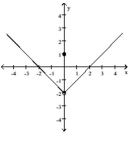
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
A
For the function f whose graph is given, determine the limit.
-Find
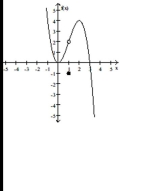
Free
(Multiple Choice)
4.8/5  (26)
(26)
Correct Answer:
D
Sketch the graph of a function y = f(x) that satisfies the given conditions.
-
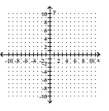
(Essay)
4.8/5  (33)
(33)
Provide an appropriate response.
-A function is continuous on . It is known to be positive at and negative at . What, if anything, does this indicate about the equation ? Illustrate with a sketch.
![Provide an appropriate response. -A function \mathrm { y } = \mathrm { f } ( \mathrm { x } ) is continuous on [ - 1,1 ] . It is known to be positive at x = - 1 and negative at x = 1 . What, if anything, does this indicate about the equation f ( x ) = 0 ? Illustrate with a sketch.](https://storage.examlex.com/TB6591/11ecd8ef_ac9b_8779_af61_a919c6aa292b_TB6591_11.jpg)
(Essay)
4.9/5  (42)
(42)
Provide an appropriate response.
-If functions and are continuous for possibly be discontinuous at a point of Provide an example.
(Essay)
4.9/5  (37)
(37)
Use the table to estimate the rate of change of y at the specified value of x.
-
x y 0 0 2 0.01 4 0.04 6 0.09 8 0.16 0 0.25 2 0.36 4 0.49
(Multiple Choice)
4.9/5  (36)
(36)
Find the slope of the curve at the given point P and an equation of the tangent line at P.
-
(Multiple Choice)
4.8/5  (37)
(37)
Sketch the graph of a function y = f(x) that satisfies the given conditions.
-
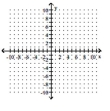
(Essay)
4.7/5  (37)
(37)
Showing 1 - 20 of 327
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)