Exam 10: Correlation and Regression
Exam 1: Introduction to Statistics155 Questions
Exam 2: Exploring Data With Tables and Graphs132 Questions
Exam 3: Describing, Exploring, and Comparing Data225 Questions
Exam 4: Probability219 Questions
Exam 5: Discrete Probability Distributions205 Questions
Exam 6: Normal Probability Distributions254 Questions
Exam 7: Estimating Parameters and Determining Sample Sizes170 Questions
Exam 8: Hypothesis Testing187 Questions
Exam 9: Inferences From Two Samples192 Questions
Exam 10: Correlation and Regression174 Questions
Exam 11: Goodness-Of-Fit and Contingency Tables100 Questions
Exam 12: Analysis of Variance113 Questions
Exam 13: Nonparametric Tests121 Questions
Exam 14: Statistical Process Control90 Questions
Select questions type
Use computer software to find the multiple regression equation. Can the equation be used for prediction? A wildlife analyst gathered the data in the table to develop an equation to predict the weights of bears. He used
WEIGHT as the dependent variable and CHEST, LENGTH, and SEX as the independent variables. For SEX, he
Used male = 1 and female = 2. WEIGHT CHEST LENGTH SEX 344 45.0 67.5 1 416 54.0 72.0 1 220 41.0 70.0 2 360 49.0 68.5 1 332 44.0 73.0 1 140 32.0 63.0 2 436 48.0 72.0 1 132 33.0 61.0 2 356 48.0 64.0 2 150 35.0 59.0 1 202 40.0 63.0 2 365 50.0 70.5 1
(Multiple Choice)
4.9/5  (35)
(35)
The table below lists weights (carats) and prices (dollars) for randomly selected diamonds. Is there sufficient
evidence to suggest that there is a linear correlation between weights and prices? Construct a scatterplot, and
find the value of the linear correlation coefficient r.
Also find the P-value or the critical values of r using Weight 0.3 0.4 0.5 0.5 1.0 0.7 Price 510 1151 1343 1410 5669 2277
(Essay)
4.9/5  (41)
(41)
The table below lists weights (carats) and prices (dollars) for randomly selected diamonds. Find the regression
equation, letting the weight be the predictor variable. Find the best predicted price for a diamond with a weight
of 1.50 carats. What is wrong with predicting the price of a 1.50-carat diamond? Weight 0.3 0.4 0.5 0.5 1.0 0.7 Price 510 1151 1343 1410 5669 2277
(Essay)
4.8/5  (43)
(43)
Use computer software to find the best multiple regression equation to explain the variation in the dependent variable, Y, in terms of the independent variables,
- 344 45.0 67.5 1 CORRELATION COEFFICIENTS 416 54.0 72.0 1 /=0.951 220 41.0 70.0 2 /=0.789 360 49.0 68.5 1 /=-0.616 332 44.0 73.0 1 140 32.0 63.0 2 436 48.0 72.0 1 132 33.0 61.0 2 =0.905 356 48.0 64.0 2 ,=0.919 150 35.0 59.0 1 ,,=0.927 202 40.0 63.0 2 365 50.0 70.5 1
(Multiple Choice)
4.7/5  (41)
(41)
Use the computer display to answer the question.
-A collection of paired data consists of the number of years that students have studied Spanish and their scores on a Spanish language proficiency test. A computer program was used to obtain the least squares linear
Regression line and the computer output is shown below. Along with the paired sample data, the program was
Also given an x value of 2 (years of study) to be used for predicting test score.
The regression equation is
Predictor Coef StDev Constant 31.55 6.360 4.96 0.000 Years 10.90 1.744 6.25 0.000
Fit StDev Fit 95.0\% CI 95.0\% PI 53.35 3.168 (42.72,63.98) (31.61,75.09)
What percentage of the total variation in test scores can be explained by the linear relationship between years of
Study and test scores?
(Multiple Choice)
4.7/5  (32)
(32)
The results for several randomly selected students for test 1 and test 2 grades are given below. Test 1 59 63 65 69 58 77 76 69 70 64 Test 2 72 67 78 82 75 87 92 83 87 78 Is there sufficient evidence to suggest that there is a linear correlation between test 1 and test 2 grades? Construct a
scatterplot, and find the value of the linear correlation coefficient r. Also, find the P-value or the critical value(s) of r
using
(Essay)
4.8/5  (33)
(33)
Find the unexplained variation for the paired data. The equation of the regression line for the paired data below is 2 4 5 6 7 11 13 20
(Multiple Choice)
4.9/5  (42)
(42)
Construct a scatterplot and identify the mathematical model that best fits the data. Assume that the model is to be used
only for the scope of the given data and consider only linear, quadratic, logarithmic, exponential, and power models. Use
a calculator or computer to obtain the regression equation of the model that best fits the data. You may need to fit several
models and compare the values of
- 1 2 3 4 5 7 17 20 25 28
(Multiple Choice)
4.8/5  (39)
(39)
Use computer software to find the best multiple regression equation to explain the variation in the dependent variable, Y, in terms of the independent variables,
-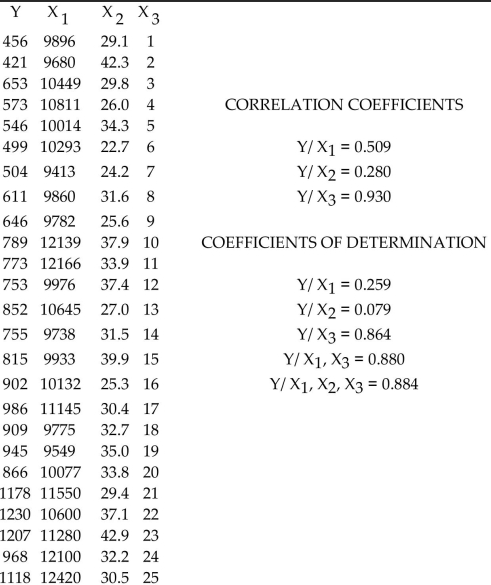
(Multiple Choice)
4.9/5  (43)
(43)
The table lists the value y (in dollars) of $100 deposited in a certificate of deposit (CD) at a bank after y years. Year 1 2 3 4 5 20 Value 103 106.09 109.27 112.55 115.93 180.61 Construct a scatterplot and identify the mathematical model that best fits the given data. Assume that the model
is to be used only for the scope of the given data, and consider only linear, quadratic, logarithmic, exponential,
and power models. Include the type of model and the equation for the model you find.
(Essay)
4.8/5  (45)
(45)
Use the given data to find the equation of the regression line. Round the final values to three significant digits, if necessary. 6 8 20 28 36 2 4 13 20 30
(Multiple Choice)
4.8/5  (30)
(30)
Suppose you will perform a test to determine whether there is sufficient evidence to support a claim of a linear
correlation between two variables. Find the critical values of r given the number of pairs of data n and the significance
level
-Nine pairs of data yield and the regression equation Also, . What is the best predicted value of for ?
(Multiple Choice)
4.8/5  (35)
(35)
The following residual plot is obtained after a regression equation is determined for a set of data. Does the
residual plot suggest that the regression equation is a bad model? Why or why not? 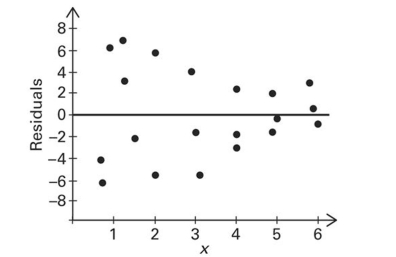
(Essay)
4.8/5  (33)
(33)
Suppose you will perform a test to determine whether there is sufficient evidence to support a claim of a linear correlation between two variables. Find the critical value(s) of r given that n = 15 and
(Multiple Choice)
4.8/5  (37)
(37)
Suppose you will perform a test to determine whether there is sufficient evidence to support a claim of a linear
correlation between two variables. Find the critical values of r given the number of pairs of data n and the significance
level
-Given: There is no significant linear correlation between scores on a math test and scores on a verbal test.
Conclusion: There is no relationship between scores on the math test and scores on the verbal test.
(Essay)
4.9/5  (42)
(42)
Use the given data to find the equation of the regression line. Round the final values to three significant digits, if necessary. Two different tests are designed to measure employee productivity and dexterity. Several employees
Are randomly selected and tested with these results. Productivity (x) 23 25 28 21 21 25 26 30 34 36 Dexterity (y) 49 53 59 42 47 53 55 63 67 75
(Multiple Choice)
4.8/5  (33)
(33)
Describe what scatterplots are and discuss the importance of creating scatterplots.
(Essay)
4.8/5  (34)
(34)
Suppose you will perform a test to determine whether there is sufficient evidence to support a claim of a linear
correlation between two variables. Find the critical values of r given the number of pairs of data n and the significance
level
-Eight pairs of data yield and the regression equation Also, . What is the best predicted value of for ?
(Multiple Choice)
4.9/5  (38)
(38)
Give an example of a pair of variables which you would expect to have a negative linear correlation coefficient
and explain why.
(Essay)
4.8/5  (33)
(33)
Showing 121 - 140 of 174
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)