Exam 6: Slope Fields and Eulers Method
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Use integration to find a general solution of the differential equation
(Multiple Choice)
4.8/5  (26)
(26)
The initial investment in a savings account in which interest is compounded continuously is . If the time required to double the amount is years, what is the amount after 15 years? Round your answer to the nearest cent.
(Multiple Choice)
4.8/5  (33)
(33)
where is weight in pounds and is time in years. What is the maximum weight of the animal if one uses the model ?
(Multiple Choice)
4.8/5  (41)
(41)
The half life of the radium isotope Ra-226 is approximately 1,599 years. If the amount left after 1,000 years is 1.8 g, what is the amount after 2000 years? Round your answer to Three decimal places.
(Multiple Choice)
4.7/5  (38)
(38)
Find the particular solution of the differential equation satisfies the boundary condition .
(Multiple Choice)
4.9/5  (40)
(40)
Sketch a few solutions of the differential equation on the slope field and then find the general solution analytically.
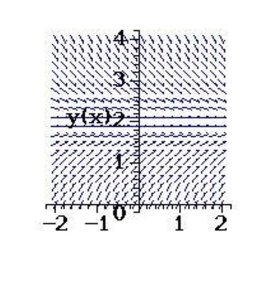
(Multiple Choice)
4.9/5  (38)
(38)
A conservation organization releases 30 panthers into a preserve. After 3 years, there are 50 panthers in the preserve. The preserve has a carrying capacity of 150. Determine the time it Takes for the population to reach 110.
(Multiple Choice)
4.9/5  (35)
(35)
Select from the choices below the slope field for the differential equation.
(Multiple Choice)
4.8/5  (35)
(35)
The half-life of the radium isotope Ra-226 is approximately 1,599 years. What percent of a given amount remains after 800 years? Round your answer to two decimal places.
(Multiple Choice)
5.0/5  (37)
(37)
The isotope has a half-life of 5,715 years. Given an initial amount of 11 grams of the isotope, how many grams will remain after 500 years? After 5,000 years? Round your answers to four decimal places.
(Multiple Choice)
4.8/5  (44)
(44)
A 300-gallon tank is full of a solution containing 35 pounds of concentrate. Starting at time distilled water is added to the tank at a rate of 30 gallons per minute, and the well-stirred Solution is withdrawn at the same rate. Find the amount of concentrate Q in the solution as a function Of t.
(Multiple Choice)
4.7/5  (35)
(35)
the initial condition when , where is the general solution.
(Multiple Choice)
4.9/5  (28)
(28)
Showing 21 - 40 of 85
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)