Exam 16: Vector Calculus
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
Evaluate the line integral
where and is the arc of the circle traversed counterclockwise from to . Round your answer to two decimal places.
(Multiple Choice)
5.0/5  (40)
(40)
Determine whether or not is a conservative vector field. If it is, find a function such that
(Short Answer)
4.9/5  (34)
(34)
Use Green's Theorem to find the work done by the force
in moving a particle in the positive direction once around the triangle with vertices , and .
Select the correct answer.
(Multiple Choice)
4.8/5  (49)
(49)
Find the gradient vector field of . Select the correct answer.
(Multiple Choice)
4.8/5  (33)
(33)
The plot of a vector field is shown below. A particle is moved from the point to . By inspection, determine whether the work done by on the particle is positive, negative, or zero.
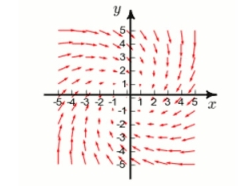
(Short Answer)
4.8/5  (36)
(36)
Evaluate the surface integral.
is the part of the plane that lies in the first octant.
(Short Answer)
4.7/5  (33)
(33)
Evaluate the surface integral where is the surface with parametric equations ,
,
(Short Answer)
4.9/5  (39)
(39)
Find the gradient vector field of the scalar function . (That is, find the conservative vector field for the potential function of .)
(Short Answer)
4.8/5  (33)
(33)
Consider the vector field
If a particle starts at the point in the velocity field given by , find an equation of the path it follows.
(Short Answer)
4.9/5  (31)
(31)
Evaluate the surface integral. Round your answer to four decimal places.
is surface .
(Multiple Choice)
4.7/5  (24)
(24)
Calculate the work done by the force field when a particle moves under its influence around the edge of the part of the sphere that lies in the first octant, in a counterclockwise direction as viewed from above.
(Short Answer)
4.9/5  (30)
(30)
Find the area of the part of the surface that lies between the planes , and .
(Short Answer)
4.9/5  (36)
(36)
Find parametric equations for , if is the curve of intersection of the hyperbolic paraboloid and the cylinder oriented counterclockwise as viewed from above.
(Short Answer)
4.9/5  (28)
(28)
Find the divergence of the vector field .
Select the correct answer.
(Multiple Choice)
4.7/5  (27)
(27)
Below is given the plot of a vector field in the -plane. (The -component of is 0 .) By studying the plot, determine whether is positive, negative, or zero.
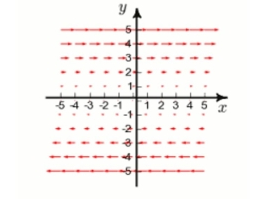
(Short Answer)
4.8/5  (39)
(39)
A plane lamina with constant density occupies a region in the -plane bounded by a simple closed path . Its moments of inertia about the axes are
Find the moments of inertia about the axes, if is a rectangle with vertices , and
(Short Answer)
4.8/5  (32)
(32)
Evaluate the surface integral where is the surface with parametric equations ,
Select the correct answer.
(Multiple Choice)
4.8/5  (39)
(39)
Showing 121 - 140 of 159
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)