Exam 16: Vector Calculus
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
Find the mass of the surface having the given mass density.
is part of the plane in the first octant; the density at a point on is equal to the square of the distance between and the -plane.
(Multiple Choice)
4.8/5  (35)
(35)
Use Green's Theorem to find the work done by the force
in moving a particle in the positive direction once around the triangle with vertices , and .
(Short Answer)
4.7/5  (31)
(31)
Below is given the plot of a vector field in the -plane. (The -component of is 0 .) By studying the plot, determine whether is positive, negative, or zero.
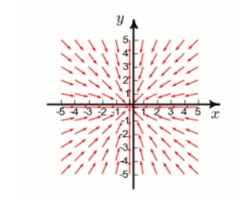
(Multiple Choice)
4.8/5  (39)
(39)
Find the work done by the force field on a particle that moves along the parabola from to .
(Multiple Choice)
4.8/5  (39)
(39)
Find the value of the constant such that the vector field
is the curl of some vector field .
(Short Answer)
4.9/5  (29)
(29)
Use Stoke's theorem to evaluate , where and is the boundary of the part of the plane in the first octant. Select the correct answer.
(Multiple Choice)
4.8/5  (36)
(36)
Evaluate the surface integral. Round your answer to four decimal places.
is surface .
Select the correct answer.
(Multiple Choice)
4.9/5  (30)
(30)
Use the Divergence Theorem to calculate the surface integral ; that is, calculate the flux of across .
is the surface of the box bounded by the coordinate planes and the planes and .
Select the correct answer.
(Multiple Choice)
4.8/5  (27)
(27)
Find a vector representation for the surface.
The plane that passes through the point and contains the vectors and
(Short Answer)
4.7/5  (43)
(43)
Find the mass of the surface having the given mass density.
is the hemisphere ; the density at a point on is equal to the distance between and the -plane.
(Short Answer)
4.8/5  (28)
(28)
Determine whether is conservative. If so, find a function such that .
(Short Answer)
4.8/5  (39)
(39)
Let be the cube with vertices . Approximate by using a
Riemann sum as in Definition 1, taking the patches to be the squares that are the faces of the cube and the points to be the centers of the squares.
(Multiple Choice)
4.7/5  (35)
(35)
Determine whether or not vector field is conservative. If it is conservative, find a function such that .
(Short Answer)
4.9/5  (34)
(34)
Showing 21 - 40 of 159
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)