Exam 2: Circuit Laws
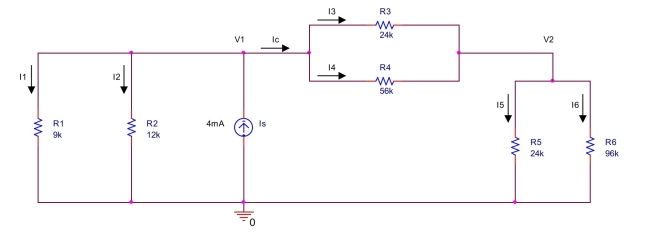
the circuit shown below,
(a) Find the equivalent resistances Ra = R3 || R4, Rb = R5 || R6, and Rc = Ra + Rb.
(b) Redraw the circuit consisting of Is, R1, R2, Rc.
(c) Use the current divider rule to find the currents I1, I2, Ic.
(d) Use the current divider rule to find the currents I3, I4, I5, I6.
(e) Find the voltages V1, V2.
![\text { (a) } \mathrm { R } _ { \mathrm { a } } = \mathrm { R } _ { 3 } \left\| \mathrm { R } _ { 4 } = 16.8 \mathrm { k } \Omega , \mathrm { R } _ { \mathrm { b } } = \mathrm { R } _ { 5 } \right\| \mathrm { R } _ { 6 } = 19.2 \mathrm { k } \Omega , \mathrm { R } _ { \mathrm { c } } = \mathrm { R } _ { \mathrm { a } } + \mathrm { R } _ { \mathrm { b } } = 36 \mathrm { k } \Omega (c) I _ { 1 } = I _ { s } \times \frac { \frac { 1 } { R _ { 1 } } } { \frac { 1 } { R _ { 1 } } + \frac { 1 } { R _ { 2 } } + \frac { 1 } { R _ { c } } } = 4 \mathrm {~mA} \times \frac { \frac { 1 } { 9000 } } { \frac { 1 } { 9000 } + \frac { 1 } { 12000 } + \frac { 1 } { 36000 } } = 4 \mathrm {~mA} \times \frac { \frac { 36000 } { 9000 } } { \frac { 36000 } { 9000 } + \frac { 36000 } { 12000 } + \frac { 36000 } { 36000 } } = 4 \mathrm {~mA} \times \frac { 4 } { 4 + 3 + 1 } = 2 \mathrm {~mA} I _ { 2 } = I _ { s } \times \frac { \frac { 1 } { R _ { 2 } } } { \frac { 1 } { R _ { 1 } } + \frac { 1 } { R _ { 2 } } + \frac { 1 } { R _ { c } } } = 4 \mathrm {~mA} \times \frac { \frac { 1 } { 12000 } } { \frac { 1 } { 9000 } + \frac { 1 } { 12000 } + \frac { 1 } { 36000 } } = 4 \mathrm {~mA} \times \frac { \frac { 36000 } { 12000 } } { \frac { 36000 } { 9000 } + \frac { 36000 } { 12000 } + \frac { 36000 } { 36000 } } = 4 \mathrm {~mA} \times \frac { 3 } { 4 + 3 + 1 } = 1.5 \mathrm {~mA} I _ { c } = I _ { s } \times \frac { \frac { 1 } { R _ { c } } } { \frac { 1 } { R _ { 1 } } + \frac { 1 } { R _ { 2 } } + \frac { 1 } { R _ { c } } } = 4 \mathrm {~mA} \times \frac { \frac { 1 } { 36000 } } { \frac { 1 } { 9000 } + \frac { 1 } { 12000 } + \frac { 1 } { 36000 } } = 4 \mathrm {~mA} \times \frac { \frac { 36000 } { 36000 } } { \frac { 36000 } { 9000 } + \frac { 36000 } { 12000 } + \frac { 36000 } { 36000 } } = 4 \mathrm {~mA} \times \frac { 1 } { 4 + 3 + 1 } = 0.5 \mathrm {~mA} (d) I _ { 3 } = I _ { c } \times \frac { R _ { 4 } } { R _ { 3 } + R _ { 4 } } = 0.5 \mathrm {~mA} \times \frac { 56 } { 24 + 56 } k \Omega = 0.35 \mathrm {~mA} \begin{array} { l } I _ { 4 } = I _ { c } \times \frac { R _ { 3 } } { R _ { 3 } + R _ { 4 } } = 0.5 \mathrm {~mA} \times \frac { 24 } { 24 + 56 } \mathrm { k } \Omega = 0.15 \mathrm {~mA} \\ I _ { 5 } = I _ { c } \times \frac { R _ { 6 } } { R _ { 5 } + R _ { 6 } } = 0.5 \mathrm {~mA} \times \frac { 96 } { 24 + 96 } k \Omega = 0.4 \mathrm {~mA} \\ I _ { 6 } = I _ { c } \times \frac { R _ { 5 } } { R _ { 5 } + R _ { 6 } } = 0.5 \mathrm {~mA} \times \frac { 24 } { 24 + 96 } k \Omega = 0.1 \mathrm {~mA} \end{array} (e) \begin{array} { l } \mathrm { V } _ { 1 } = \mathrm { R } _ { 1 } \mathrm { I } _ { 1 } = 9 \mathrm { k } \Omega \times 2 \mathrm {~mA} = 18 \mathrm {~V} \\ \mathrm {~V} _ { 2 } = \mathrm { R } _ { 5 } \mathrm { I } _ { 5 } = 24 \mathrm { k } \Omega \times 0.4 \mathrm {~mA} = 9.6 \mathrm {~V} \end{array} clear all;format long; Is=4e-3; R1=9000;R2=12000;R3=24000;R4=56000;R5=24000;R6=96000; Ra=P([R3,R4]) Rb=P([R5,R6]) Rc=Ra+Rb I1=Is/R1/(1/R1+1/R2+1/Rc) I2=Is/R2/(1/R1+1/R2+1/Rc) Ic=Is/Rc/(1/R1+1/R2+1/Rc) I3=Ic/R3/(1/R3+1/R4) I4=Ic/R4/(1/R3+1/R4) I5=Ic/R5/(1/R5+1/R6) I6=Ic/R6/(1/R5+1/R6) V1=R1*I1 V2=R5*I5 VR3=R3*I3 Vloop=-V1+VR3+V2 Answers: Ra =16800 Rb =19200 Rc =36000 I1 =0.002000000000000 I2 =0.001500000000000 Ic =5.000000000000000e-04 I3 =3.500000000000000e-04 I4 =1.500000000000000e-04 I5 =4.000000000000001e-04 I6 =1.000000000000000e-04 V1 =18 V2 =9.600000000000001 VR3 =8.400000000000000 Vloop =1.776356839400251e-15](https://storage.examlex.com/TB8726/11ecc070_653b_c9d3_9ec6_49096e93e8b9_TB8726_11.jpg)
(c)
(d)
(e)
clear all;format long;
Is=4e-3;
R1=9000;R2=12000;R3=24000;R4=56000;R5=24000;R6=96000;
Ra=P([R3,R4])
Rb=P([R5,R6])
Rc=Ra+Rb
I1=Is/R1/(1/R1+1/R2+1/Rc)
I2=Is/R2/(1/R1+1/R2+1/Rc)
Ic=Is/Rc/(1/R1+1/R2+1/Rc)
I3=Ic/R3/(1/R3+1/R4)
I4=Ic/R4/(1/R3+1/R4)
I5=Ic/R5/(1/R5+1/R6)
I6=Ic/R6/(1/R5+1/R6)
V1=R1*I1
V2=R5*I5
VR3=R3*I3
Vloop=-V1+VR3+V2
Answers:
Ra =16800
Rb =19200
Rc =36000
I1 =0.002000000000000
I2 =0.001500000000000
Ic =5.000000000000000e-04
I3 =3.500000000000000e-04
I4 =1.500000000000000e-04
I5 =4.000000000000001e-04
I6 =1.000000000000000e-04
V1 =18
V2 =9.600000000000001
VR3 =8.400000000000000
Vloop =1.776356839400251e-15
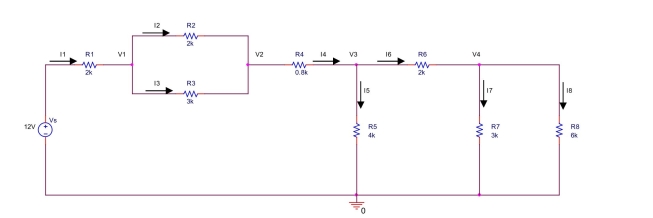
the circuit shown below,
(a) Find Ra = R7 || R8.
(b) Find Rb = R6 + Ra.
(c) Find Rc = R5 || Rb.
(d) Find Rd = R2 || R3.
(e) Redraw the circuit consisting of Vs, R1, Rd, R4, and Rc. Find the equivalent resistance Req
seen from the voltage source.
(f) Find the current I1 through R1, Rd, R4, and Rc.
(g) Find the voltage across R1, voltage across Rd, voltage across R4, and voltage across Rc.
(h) Find the voltage V1, voltage V2, and voltage V3.
(i) Find the currents I5 and I6.
(j) Find the voltage V4, and currents I7 and I8.
(a)
(b)
(c)
(d)
(e) ![(a) \mathrm { R } _ { \mathrm { a } } = \mathrm { R } _ { 7 } \| \mathrm { R } _ { 8 } = 2 \mathrm { k } \Omega (b) R _ { b } = R _ { 6 } + R _ { a } = 4 \mathrm { k } \Omega (c) \mathrm { R } _ { \mathrm { c } } = \mathrm { R } _ { 5 } \| \mathrm { R } _ { \mathrm { b } } = 2 \mathrm { k } \Omega (d) \mathrm { R } _ { \mathrm { d } } = \mathrm { R } _ { 2 } \| \mathrm { R } _ { 3 } = 1.2 \mathrm { k } \Omega (e) R _ { \text {eq } } = R _ { 1 } + R _ { d } + R _ { 4 } + R _ { c } = 6 \mathrm { k } \Omega (f) I _ { 1 } = V _ { s } / R _ { e q } = 12 \mathrm {~V} / 6 \mathrm { k } \Omega = 2 \mathrm {~mA} (g) V _ { R 1 } = R _ { 1 } I _ { 1 } = 2 \mathrm { k } \Omega \times 2 \mathrm {~mA} = 4 \mathrm {~V} V _ { \mathrm { Rd } } = \mathrm { R } _ { \mathrm { d } 1 } \mathrm { I } _ { 1 } = 1.2 \mathrm { k } \Omega \times 2 \mathrm {~mA} = 2.4 \mathrm {~V} V _ { R 4 } = R _ { 4 } I _ { 1 } = 0.8 \mathrm { k } \Omega \times 2 \mathrm {~mA} = 1.6 \mathrm {~V} V _ { R _ { c } } = R _ { c } I _ { 1 } = 2 \mathrm { k } \Omega \times 2 \mathrm {~mA} = 4 \mathrm {~V} (h) V _ { 1 } = V _ { s } - V _ { R 1 } = 12 \mathrm {~V} - 4 \mathrm {~V} = 8 \mathrm {~V} V _ { 2 } = V _ { 1 } - V _ { R d } = 8 \mathrm {~V} - 2.4 \mathrm {~V} = 5.6 \mathrm {~V} V _ { 3 } = V _ { 2 } - V _ { R 4 } = 5.6 \mathrm {~V} - 1.6 \mathrm {~V} = 4 \mathrm {~V} (i) \begin{array} { l } I _ { 5 } = \frac { V _ { 3 } } { R _ { 5 } } = \frac { 4 \mathrm {~V} } { 4 k \Omega } = 1 \mathrm {~mA} \\ I _ { 6 } = \frac { V _ { 3 } } { R _ { b } } = \frac { 4 \mathrm {~V} } { 4 k \Omega } = 1 \mathrm {~mA} \end{array} (j) \begin{array} { l } \mathrm { V } _ { 4 } = \mathrm { V } _ { 3 } - \mathrm { R } _ { 6 } \mathrm { I } _ { 6 } = 4 \mathrm {~V} - 2 \mathrm { k } \Omega \times 1 \mathrm {~mA} = 4 \mathrm {~V} - 2 \mathrm {~V} = 2 \mathrm {~V} \\ I _ { 7 } = \frac { V _ { 4 } } { R _ { 7 } } = \frac { 2 \mathrm {~V} } { 3 k \Omega } = 0.6667 \mathrm {~mA} \\ I _ { 8 } = \frac { V _ { 4 } } { R _ { 8 } } = \frac { 2 \mathrm {~V} } { 6 k \Omega } = 0.3333 \mathrm {~mA} \end{array} Vs=12; R1=2000;R2=2000;R3=3000;R4=800;R5=4000;R6=2000;R7=3000;R8=6000; Ra=P([R7,R8]) Rb=R6+Ra Rc=P([R5,Rb]) Rd=P([R2,R3]) Req=R1+Rd+R4+Rc I1=Vs/Req VR1=R1*I1 VRd=Rd*I1 VR4=R4*I1 VRc=Rc*I1 Sum1=VR1+VRd+VR4+VRc V1=Vs-VR1 V2=Vs-VR1-VRd V3=V2-VR4 I5=V3/R5 I6=V3/Rb V4=V3-R6*I6 I7=V4/R7 I8=V4/R8 Answers: Ra =2000 Rb =4000 Rc =2000 Rd =1200 Req =6000 I1 =0.002000000000000 VR1 =4 VRd =2.400000000000000 VR4 =1.600000000000000 VRc =4 Sum1 =12 V1 =8 V2 =5.600000000000000 V3 =4.000000000000000 I5 =9.999999999999998e-04 I6 =9.999999999999998e-04 V4 =2 I7 =6.666666666666666e-04 I8 =3.333333333333333e-04](https://storage.examlex.com/TB8726/11ecc070_4f07_6e82_9ec6_41e69cb21aa6_TB8726_11.jpg)
(f)
(g)
(h)
(i)
(j)
Vs=12;
R1=2000;R2=2000;R3=3000;R4=800;R5=4000;R6=2000;R7=3000;R8=6000;
Ra=P([R7,R8])
Rb=R6+Ra
Rc=P([R5,Rb])
Rd=P([R2,R3])
Req=R1+Rd+R4+Rc
I1=Vs/Req
VR1=R1*I1
VRd=Rd*I1
VR4=R4*I1
VRc=Rc*I1
Sum1=VR1+VRd+VR4+VRc
V1=Vs-VR1
V2=Vs-VR1-VRd
V3=V2-VR4
I5=V3/R5
I6=V3/Rb
V4=V3-R6*I6
I7=V4/R7
I8=V4/R8
Answers:
Ra =2000
Rb =4000
Rc =2000
Rd =1200
Req =6000
I1 =0.002000000000000
VR1 =4
VRd =2.400000000000000
VR4 =1.600000000000000
VRc =4
Sum1 =12
V1 =8
V2 =5.600000000000000
V3 =4.000000000000000
I5 =9.999999999999998e-04
I6 =9.999999999999998e-04
V4 =2
I7 =6.666666666666666e-04
I8 =3.333333333333333e-04
circuit is shown in Figure 1. In this figure,
(a) Label all the nodes (1, 2, 3, ...) in the circuit excluding the ground node which is already
labeled as 0.
(b) How many nodes are there?
(c) How many simple nodes are there?
(d) How many essential nodes are there?
(e) How many branches are there?
(f) How many meshes are there? List all meshes.
(g) How many loops (including meshes) are there?
(h) List all loops that are not meshes. 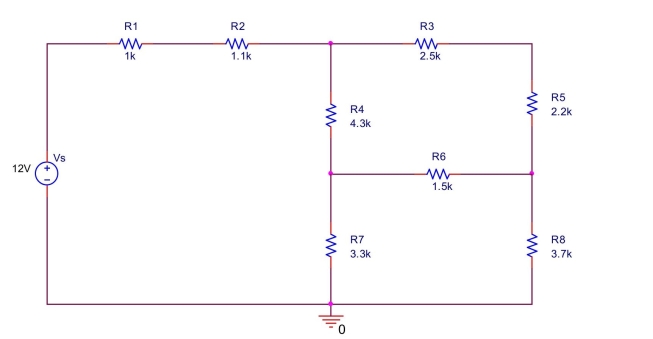 Figure 1
Figure 1
(a)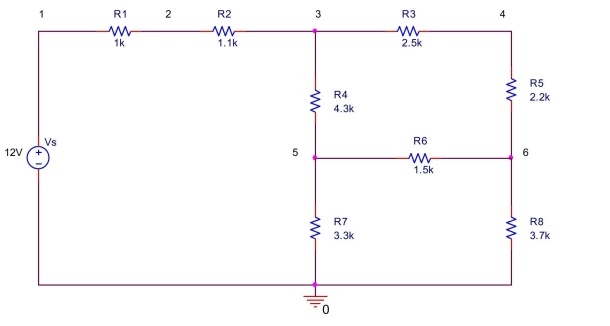
(b)There are 7 nodes (0, 1, 2, 3, 4, 5, 6).
(c)There are 3 simple nodes (1, 2, 4). Simple node connects two elements.
(d)There are 4 essential nodes (1, 2, 4). Essential node connects three or more elements.
(e)There are 9 branches.
(f)There are three meshes:
Vs - R1 - R2 - R4 - R7
R4 - R3 - R5 - R6
R7 - R6 - R8
(g)There are 7 loops.
(h)Vs - R1 - R2 - R3 - R5 - R8
Vs - R1 - R2 - R3 - R5 - R6 - R7
Vs - R1 - R2 - R4 - R6 - R8
R7 - R4 - R3 - R5 - R8
the equivalent resistance between terminals a and b of the circuit shown below. 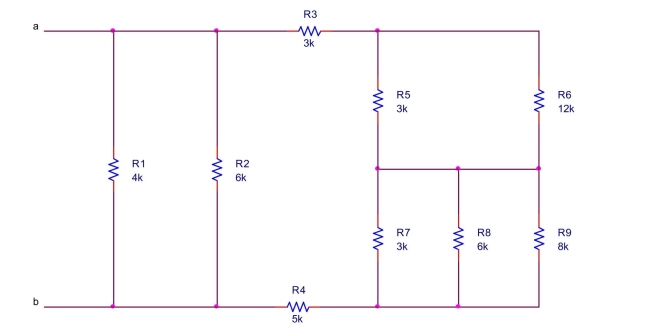
the circuit shown below, find the currents I1,I2, and I3. Also, find the powers on R1,R2, R3,and Vs and state whether power is absorbed or released by each element. 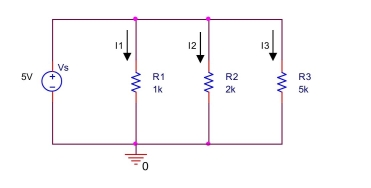
the circuit shown below,
(a) Find Ra = R5 || R6 and Rb = R3 || R4.
(b) Redraw the circuit consisting of Vs, R1, Rb, R4, and Ra. Find the equivalent resistance Req
seen from the voltage source.
(c) Find the current I1 through R1, Rb, R4, and Ra.
(d) Find the voltage across R1, voltage across Rb, voltage across R4, and voltage across Ra
(e) Find the voltage V1, voltage V2, and voltage V3.
(f) Find the currents I2, I3, I5 and I6.
the equivalent resistance between terminals a and b of the circuit shown below. 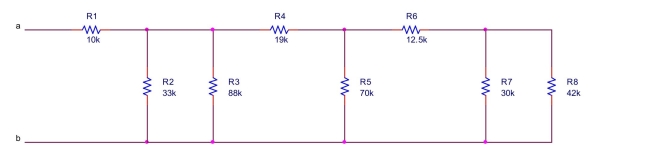
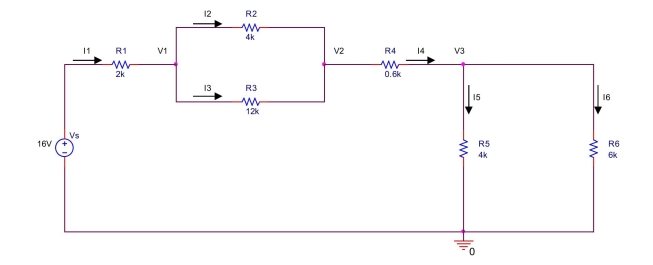
current through resistor R6 in the circuit shown below is 2 mA, that is,I6 = 2 mA.
(a) Use Ohm's law to find the voltage V4 across R6.
(b) Use Ohm's law to find the current I5 through R5.
(c) Use KCL to find the current I4 through R4.
(d) Use Ohm's law to find the voltage V3 across R4.
(e) Use KVL to find the voltage V2 across R3.
(f) Use Ohm's law to find the current I3 through R3.
(g) Use Ohm's law to find the current I2 through R2.
(h) Use KCL to find the current I1 through R1.
(i) Use Ohm's law to find the voltage V1 across R1.
(j) Use KVL to find the voltage Vs. 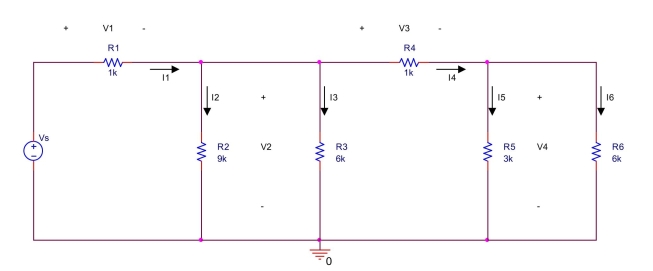
the equivalent resistance between terminals a and b of the circuit shown below. 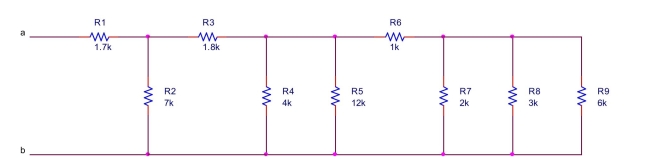
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)