Exam 6: Capacitors and Inductors
Exam 1: Voltage, Current, Power, and Sources10 Questions
Exam 2: Circuit Laws10 Questions
Exam 3: Circuit Analysis Methods20 Questions
Exam 4: Circuit Theorems13 Questions
Exam 5: Operational Amplifier Circuits7 Questions
Exam 6: Capacitors and Inductors10 Questions
Exam 7: RL and RC Circuits14 Questions
Exam 8: RLC Circuits8 Questions
Exam 9: Phasors and Impedances8 Questions
Exam 10: Analysis of Phasor Transformed Circuits15 Questions
Exam 11: AC Power5 Questions
Exam 12: Three-Phase Systems6 Questions
Exam 13: Magnetically Coupled Circuits6 Questions
Exam 14: The Laplace Transform19 Questions
Exam 15: Circuits Analysis in the S-Domain26 Questions
Select questions type
The voltage across an inductor with inductance of 510 mH is given by Find the current through the inductor i(t) and plot the voltage and current as a function of time.
Free
(Essay)
4.7/5  (30)
(30)
Correct Answer:
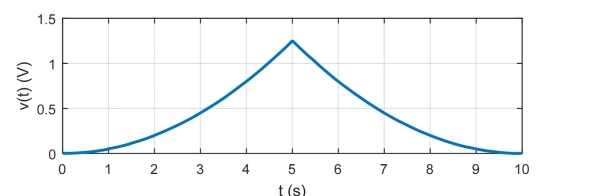
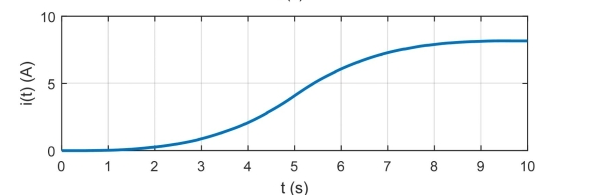
voltage across a capacitor with capacitance of 39 is given by Find the current through the capacitor i(t) and plot the voltage and current as a function of time.
Free
(Essay)
4.7/5  (29)
(29)
Correct Answer:
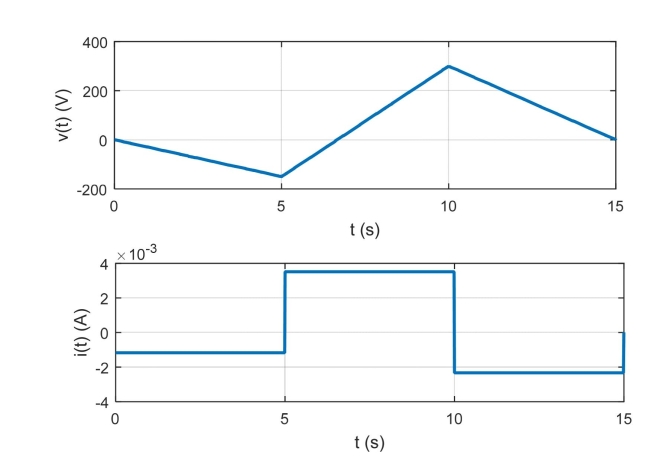
Find the equivalent capacitance between terminals a and b of the circuit shown below. 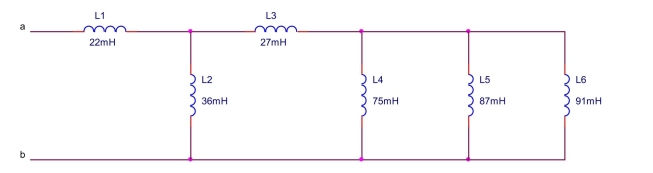
Free
(Essay)
4.7/5  (33)
(33)
Correct Answer:
clear all; format long;
find the equivalent capacitance between terminals a and b of the circuit shown below. 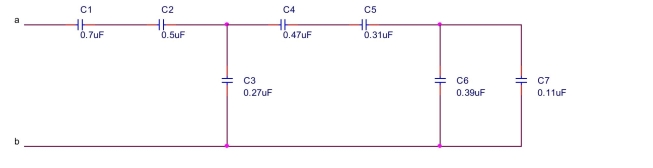
(Essay)
4.9/5  (32)
(32)
current through a capacitor with capacitance of 0.68 is given by i(t) = 4 . Find the voltage across the capacitor and plot the current and voltage as a function of time.
(Essay)
4.9/5  (35)
(35)
Find the equivalent capacitance between terminals a and b of the circuit shown below. 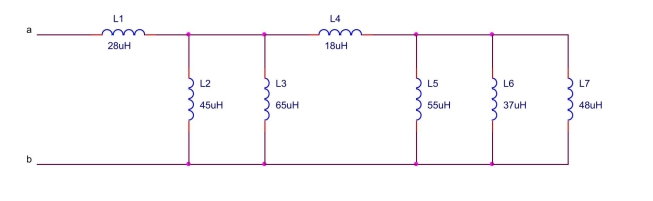
(Essay)
4.7/5  (35)
(35)
the voltage across an inductor with inductance of 39 mH is given by u(t) V. Find the current through the inductor i(t) and plot the voltage and current as a function of
time.
(Essay)
4.8/5  (32)
(32)
the current through an inductor with inductance of 430 mH is given by Find the voltage across the inductor v(t) and plot the current and voltage as a function of time.
(Essay)
4.9/5  (36)
(36)
find the equivalent capacitance between terminals a and b of the circuit shown below. 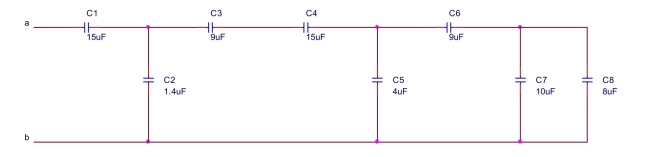
(Essay)
4.8/5  (27)
(27)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)