Exam 9: Phasors and Impedances
Exam 1: Voltage, Current, Power, and Sources10 Questions
Exam 2: Circuit Laws10 Questions
Exam 3: Circuit Analysis Methods20 Questions
Exam 4: Circuit Theorems13 Questions
Exam 5: Operational Amplifier Circuits7 Questions
Exam 6: Capacitors and Inductors10 Questions
Exam 7: RL and RC Circuits14 Questions
Exam 8: RLC Circuits8 Questions
Exam 9: Phasors and Impedances8 Questions
Exam 10: Analysis of Phasor Transformed Circuits15 Questions
Exam 11: AC Power5 Questions
Exam 12: Three-Phase Systems6 Questions
Exam 13: Magnetically Coupled Circuits6 Questions
Exam 14: The Laplace Transform19 Questions
Exam 15: Circuits Analysis in the S-Domain26 Questions
Select questions type
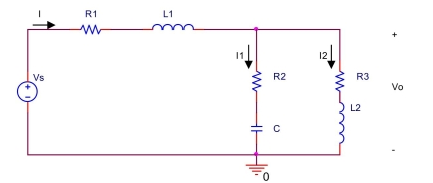
for the circuit shown below, let ,
(a) Find impedances , and phasor for .
(b) Find the equivalent impedance of parallel combination of and .
(c) Find the total impedance seen from the voltage source.
(d) Find the phasor for the current .
(e) Find the phasor for load voltage .
(f) Find the phasors for and .
Free
(Essay)
4.9/5  (36)
(36)
Correct Answer:
clear all;
;
*
(Il)
I
Find V in polar notation.
Free
(Essay)
4.8/5  (25)
(25)
Correct Answer:
clear all;
V1-P2Rd (11, 110)
V1p=R2P (V1)
V2=P2Rd (17, -75 )
V2p=R2P (V2)
V=V1+V2
Vp-R2P (V)
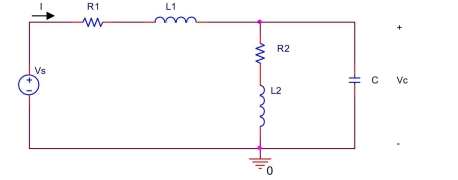
for the circuit shown below, let
(a) Find impedances , ZL2, Z and phasor for vs(t).
(b) Find the equivalent impedance of parallel combination of and .
(c) Find the total impedance seen from the voltage source.
(d) Find the phasor for the current I.
(e) Find the phasor for across the capacitor.
(f) Find .
Free
(Essay)
4.9/5  (25)
(25)
Correct Answer:
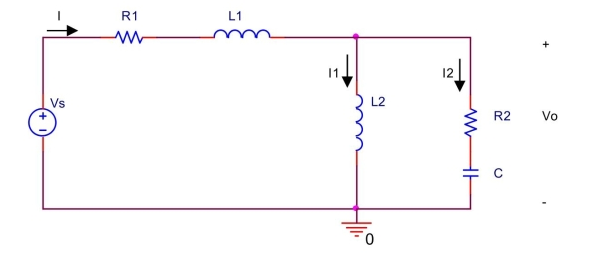
for the circuit shown below, let ()=545 2\pi60-6 ,=20\Omega,=33\Omega,=63,=72 , =128\mu
(a) Find impedances , and .
(b) Find the equivalent impedance of parallel combination of and .
(c) Find the total impedance seen from the voltage source.
(d) Find the phasor for the current I.
(e) Find the phasor for across the inductor .
(f) Find the phasors for and .
(g) Find .
(Essay)
4.8/5  (35)
(35)
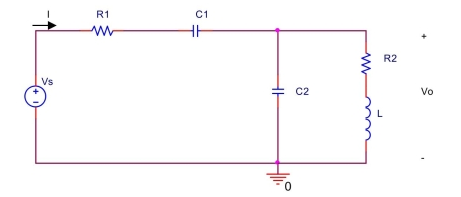
for the circuit shown below, let ()=575 2\pi60+3 =35\Omega,=53\Omega,=76,=117\mu,=106\mu (a) Find impedances , and phasor for .
(b) Find the equivalent impedance of parallel combination of and .
(c) Find the total impedance seen from the voltage source.
(d) Find the phasor for the current I.
(e) Find the phasor for across the capacitor .
(Essay)
4.7/5  (30)
(30)
Represent V in polar notation, and find the time domain expression v(t) for the voltage when
the frequency is f = 60 Hz.
(Essay)
4.8/5  (31)
(31)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)