Exam 3: Circuit Analysis Methods
Exam 1: Voltage, Current, Power, and Sources10 Questions
Exam 2: Circuit Laws10 Questions
Exam 3: Circuit Analysis Methods20 Questions
Exam 4: Circuit Theorems13 Questions
Exam 5: Operational Amplifier Circuits7 Questions
Exam 6: Capacitors and Inductors10 Questions
Exam 7: RL and RC Circuits14 Questions
Exam 8: RLC Circuits8 Questions
Exam 9: Phasors and Impedances8 Questions
Exam 10: Analysis of Phasor Transformed Circuits15 Questions
Exam 11: AC Power5 Questions
Exam 12: Three-Phase Systems6 Questions
Exam 13: Magnetically Coupled Circuits6 Questions
Exam 14: The Laplace Transform19 Questions
Exam 15: Circuits Analysis in the S-Domain26 Questions
Select questions type
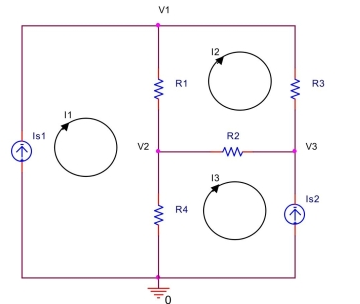
In the circuit shown below, let .
Use mesh analysis to find mesh currents , and . Also, find , and .
Free
(Essay)
4.8/5  (42)
(42)
Correct Answer:
% Mesh Analysis clear all
Isl ;
;
syms I1 I2 I3
IR
IR3
IR vpa (IR4, 7)
IR1=vpa (IR1, 7)
IR2=vpa (IR2, T)
IR3=ypa (IR3, 7)
SumI=vpa (SumI, 7) Answers:
In the circuit shown below, let
Use mesh analysis to find mesh currents , and . Also, find and . 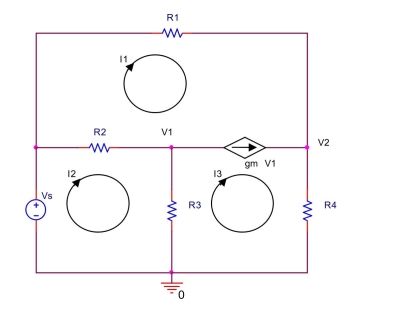
Free
(Essay)
4.9/5  (33)
(33)
Correct Answer:
% Mesh Analysis clear all
syms I1 I2 I3
IR
IRl
IR2
IR
SumI
I
IR1=Vpa (IR1, 7)
IR2 = VPa (IR2, 7)
IR3=vpa
SumI=vpa SumI, Answers:
In the circuit shown below, (a) Write a mesh equation by summing the voltage drops around mesh 1 (left side).
(b) Write a mesh equation by summing the voltage drops around mesh 2 (right side).
(c) Solve the two equations to find and .
(d) Find voltage across . 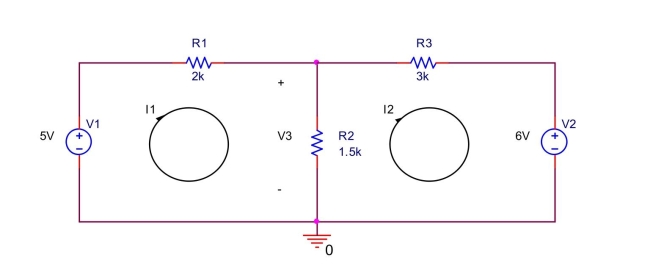
Free
(Essay)
4.8/5  (37)
(37)
Correct Answer:
% Mesh Analysis clear all
;
Answers:
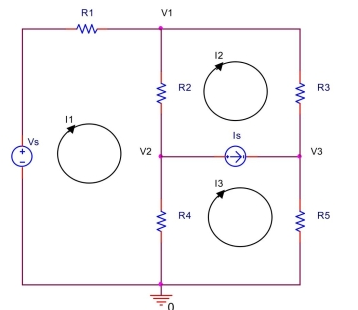
In the circuit shown below, let
Use mesh analysis to find mesh currents , and . Also, find , and .
(Essay)
4.7/5  (26)
(26)
In the circuit shown below, let
Use mesh analysis to find mesh currents , and . Also, find and . 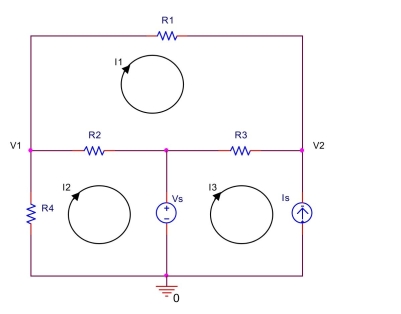
(Essay)
4.9/5  (38)
(38)
In the circuit shown below, let
Use mesh analysis to find mesh currents and . Also, find .
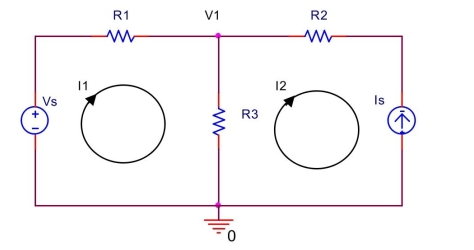
(Essay)
4.8/5  (42)
(42)
In the circuit shown below, (a) Write a mesh equation around mesh 1 by summing the voltage drops around mesh 1 .
(b) Write a mesh equation around supermesh formed by meshes 2 and 3 by summing the voltage drops around supermesh.
(c) Write a constraint equation expressing by and .
(d) Find , and by solving the three equations.
(e) Find the voltages . 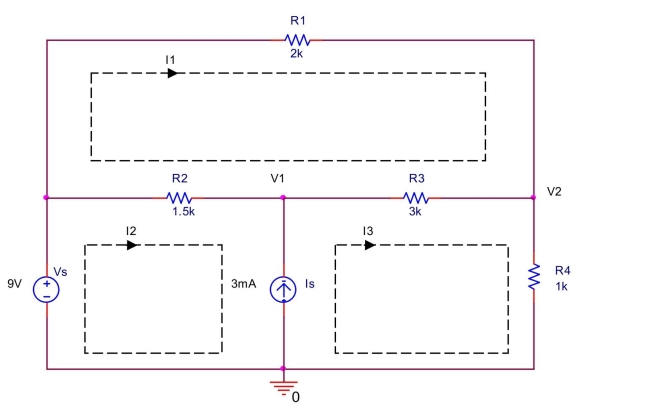
(Essay)
4.7/5  (35)
(35)
the circuit shown below, let
(a) Write a node equation at node 1 by summing the currents away from node 1 .
(b) Write a node equation at node 2 by summing the currents away from node 2 .
(c) Solve the equations to find and .
(d) Find the current through (including direction) and power absorbed by .
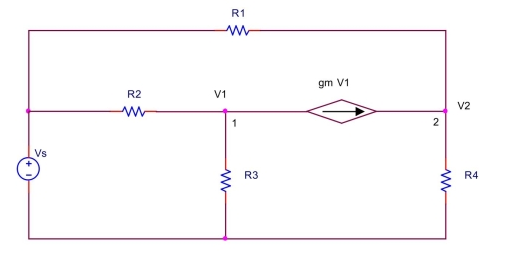
(Essay)
4.9/5  (32)
(32)
In the circuit shown below, let
Use mesh analysis to find mesh currents and . Also, find and .
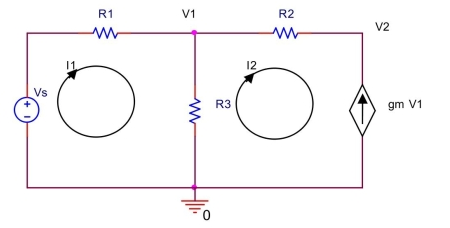
(Essay)
4.7/5  (38)
(38)
the circuit shown below, (b) Write a node equation at node 2 by summing the currents away from node
(c) Solve the equations to find and .
(d) Find the current through (including direction) and power dissipated on . 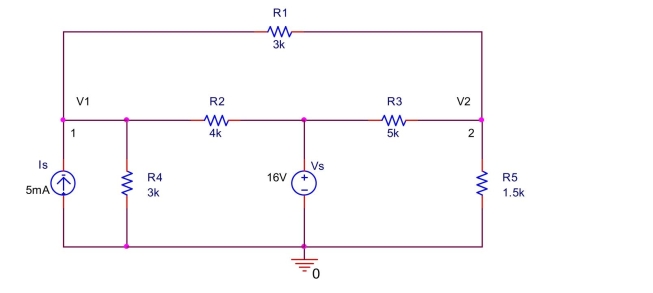
(Essay)
4.9/5  (40)
(40)
In the circuit shown below, let
Use mesh analysis to find mesh currents , and . Also, find , and . 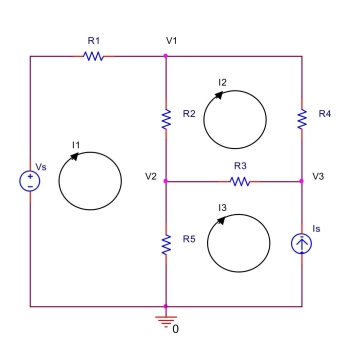
(Essay)
4.8/5  (32)
(32)
In the circuit shown below, let
Use mesh analysis to find mesh currents , and . Also, find , and .
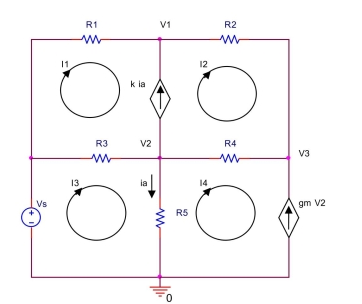
(Essay)
4.9/5  (31)
(31)
the circuit shown below, (a) Write a node equation at node 1 by summing the currents leaving node 1 .
(b) Write a node equation at node 2 by summing the currents leaving node
(c) Find and by solving the two node equations.
(d) Find the currents .
(e) Find the power absorbed by , and power released by and .
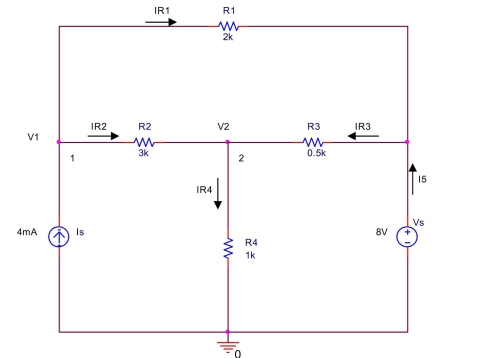
(Essay)
4.7/5  (42)
(42)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)