Exam 15: Further Topics in Algebra and Change

Write an equation for the line that passes through the points (6, ${}^ {-} 6$ ) and (1, ${}^ {-} \frac { 8 } { 3 }$ ). Simplify to the $y = m x + b$ form.

Write an equation for the line that passes through the points (2, 7) and (6, 13). Simplify to the $y = m x + b$ form.

Chicken joins Turtle and Rabbit in an over-and-back race, with known data as in the drawing below. A) Going the same speed over and back, Rabbit won the race. What was Rabbit's speed? Explain your thinking. B) What was Chicken's average speed for the whole over-and-back trip? Show your work.

Use the substitution method to find a common solution to the given equations, if there is one, or state that there is no common solution. $\left\{ \begin{array} { l } y = 7 x - 5 \\2 y - 14 x = 7\end{array} \right.$

Mr. Cool joins Rabbit and Turtle in an over-and-back race, 200 meters each way. Rabbit: speed over = 50 meters/second; time back = 10 seconds Mr. Cool: time over = 8 seconds; speed back = 40 meters/second Turtle: the same speed both ways but rested for 5 seconds after the first 200 meters A) Who finished first, Rabbit or Mr. Cool, and what was each one's time in seconds? B) What was Rabbit's average speed for the race? C) What was Turtle's speed when he was moving if Turtle tied Rabbit (remember that Turtle rested for 5 seconds)?

Write an equation for the line that is parallel to the line of $y - 3 x = 5$ and passes through the point (4, 9). Simplify to the $y = m x + b$ form.

Abe got 94 out of 100 on one test but only 26 out of 50 on a second. He figures he has 94 + 26, or 120, out of 150 and finds that to be 80%. Hence, he cannot understand why his teacher's grade book shows a different result: 94% and 52%, which give an average of $\frac { 94 \% + 52 \% } { 2 }$ = 73%. What accounts for the difference?

Wile E. was going back to his cave and spotted his cousin, waiting for him. So Wile E. started jogging toward his cave at a steady speed of 40 feet/second. After 3 seconds and while 120 feet from his cave, Wile E. sprained his ankle. How far was Wile E. from his cave when he spotted his cousin?

Write an equation for the line that is parallel to the line of $y = 7 x + 2$ and passes through the point (1, 16). Simplify to the $y = m x + b$ form.

Write an equation for the line that has slope $\frac { 1 } { 3 }$ and passes through the point (12, 6). Simplify to the $y = m x + b$ form.

Consider these three function rules: $f ( x ) = 2 x + 1 \quad g ( i n p u t ) = 4 \cdot \text { input } h ( \text { input } ) = ( \text { input } ) ^ { 2 }$ Give the final output if 2 is the input to each of the following combinations. A) The combination is [first f(x) then g(input)] and then h(output from that combination). In other words, the output of f is the input for g, and the input of that combination is the input for h. B) The output from f(x) is the input to the combination of g and h [first g(input) then h(input)]. In other words, combine g and h and use this new function to combine with f. C) What do your results from parts A and B suggest about associativity of combinations of functions? (Note to the instructor: Use this item cautiously, unless you have treated associativity.)

Wile E. joined Rabbit and Turtle in an over-and-back race, 200 meters each way. Show your work. Rabbit: speed over = 20 meters/second; time back = 4 seconds Wile E.: time over = 8 seconds; speed back = 40 meters/second Turtle: the same speed both ways A) Who of Rabbit and Wile E. finished first? B) What was Turtle's speed, if he tied Rabbit? C) Use one coordinate system to show qualitative speed versus time graphs for Rabbit's (mark with ____), Wile E.'s (mark with ......), and Turtle's (mark with ^{x x x x}) speeds over and back.

Use the substitution method to find a common solution to the given equations, if there is one, or state that there is no common solution. $\left\{ \begin{array} { l } y - 4 x = 1 \\y = 5 x - 1\end{array} \right.$

Find a function rule for the following data. t s(t) 0 0 1 16 2 64 3 144 4 256

You are on the committee planning your school's annual food fair, where parents provide food samples that people buy with food tickets. You are considering three plans for charges: Highest entry, lowest ticket price $( \mathrm { HL } ) : \$ 5$ entry, plus 504 for each food ticket Middle entry, middle ticket price (MM): $\$ 4$ entry, plus $75 \phi$ for each food ticket Low entry, highest ticket price $( \mathrm { LH } )$ : $\$ 2$ entry, plus $95 \phi$ for each food ticket Which plan do you think is best? Be sure to support your idea wit equations, a graph, a table, or quantitative analysis.

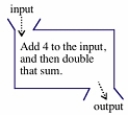
Suppose that $g ( x ) = 5 x + 2$ and h(x) is defined by machine X below. Give the output if 3 is the input to each of the following combinations. A) first h(x) then g(x) B) first g(x) then h(x)

Use the substitution method to find a common solution to the given equations, if there is one, or state that there is no common solution. $\left\{ \begin{array} { l } y = 3 x + 7 \\22 = 3 y - 10 x\end{array} \right.$

Write an equation for the line that is perpendicular to the line of $y = 4 x + 5$ and passes through the point (8, 4). Simplify to the $y = m x + b$ form.

Use the addition/subtraction method to find a common solution to the given equations, if there is one, or state that there is no common solution. $\left\{ \begin{array} { l } 2 x + 3 y = 9 \\x - y = 2\end{array} \right.$

Write an equation for the line that has slope ${}^ {-} 4$ and passes through the point (2, 1). Simplify to the $y = m x + b$ form.