Exam 15: Further Topics in Algebra and Change
Exam 1: Reasoning About Quantities34 Questions
Exam 2: Numeration Systems96 Questions
Exam 3: Understanding Whole Number Operations66 Questions
Exam 4: Some Conventional Ways of Computing17 Questions
Exam 5: Using Numbers in Sensible Ways38 Questions
Exam 6: Meanings for Fractions85 Questions
Exam 7: Computing With Fractions54 Questions
Exam 8: Multiplicative Comparisons and Multiplicative Reasoning19 Questions
Exam 9: Ratios, Rates, Proportions, and Percents33 Questions
Exam 10: Integers and Other Number Systems24 Questions
Exam 11: Number Theory57 Questions
Exam 12: What Is Algebra28 Questions
Exam 13: A Quantitative Approach to Algebra and Graphing18 Questions
Exam 14: Understanding Change: Relationships Among Time, Distance, and Rate10 Questions
Exam 15: Further Topics in Algebra and Change55 Questions
Exam 16: Polygons75 Questions
Exam 17: Polyhedra51 Questions
Exam 18: Symmetry17 Questions
Exam 19: Tessellations9 Questions
Exam 20: Similarity47 Questions
Exam 21: Curves, Constructions, and Curved Surfaces17 Questions
Exam 22: Transformation Geometry24 Questions
Exam 23: Measurement Basics21 Questions
Exam 24: Area, Surface Area, and Volume27 Questions
Exam 25: Counting Units Fast: Measurement Formulas31 Questions
Exam 26: Special Topics in Measurement21 Questions
Exam 27: Quantifying Uncertainty39 Questions
Exam 28: Determining More Complicated Probabilities37 Questions
Exam 29: Introduction to Statistics and Sampling7 Questions
Exam 30: Representing and Interpreting Data With One Variable32 Questions
Exam 31: Dealing With Multiple Data Sets or With Multiple Variables8 Questions
Exam 32: Variability in Samples21 Questions
Exam 33: Special Topics in Probability16 Questions
Select questions type
There is a (common) error, or some confusion, in each of the following situations. Find the error/confusion, and explain why some thinking was off, even though the person thought the thinking was all right.
A) Before summer school, a student had completed 96 units, with a GPA of 2.9. The student takes two three-unit courses in summer school and gets an A and a B for a 3.5 GPA. The student is pleased on calculating and finding the new GPA to be 3.2.
B) A teenager says she never has anything nice to wear. Her parents tell her she can buy four new blouses for her birthday but to keep the average price at $25 (or less). The girl finds some $40 blouses she really likes and calculates from = 25 that x = 10. So a $40 blouse and a $10 blouse would give an average of $25. She is happy to find an acceptable $10 blouse on a sale table. She buys that one and three of the $40 blouses in different colors.
C) A person bought a used car and wants to check its gas mileage. For the first few fill-ups, she covered 823 miles and got 24.4 miles/gallon. The next fill-up, after 240 more miles, took 6 gallons, so she got 40 miles/gallon. She calculates = 32.2 miles/gallon.
(Essay)
4.8/5  (37)
(37)
Write an equation for the line that has slope 3 and passes through the point (2, 7). Simplify to the
form.
(Short Answer)
4.7/5  (33)
(33)
Use the addition/subtraction method to find a common solution to the given equations, if there is one, or state that there is no common solution.
(Essay)
4.9/5  (40)
(40)
Write an equation for the line that has slope 3 and passes through the point (9, 7). Simplify to the
form.
(Short Answer)
4.7/5  (38)
(38)
Write an equation for the line that is perpendicular to the line of and passes through the point (15, 2). Simplify to the form.
(Short Answer)
4.9/5  (46)
(46)
Find a function rule for the following data.
x f(x) 90 355 91 359 92 363 93 367
(Short Answer)
4.8/5  (38)
(38)
You and your roommates want to subscribe to a movie rental service. You have two choices: Movies-R-Us charges $15/month, plus $3.50 per movie rented, and See-It-Now charges $7.95/month, plus $5 per movie rented.
A) For each choice, write an equation giving the cost c for renting n movies a month.
B) Which choice should you make, under different scenarios? (For example, you watch lots of movies, you watch only occasionally, etc.) Give your reasoning, perhaps supporting your idea with a graph.
(Essay)
4.8/5  (37)
(37)
Use the substitution method to find a common solution to the given equations, if there is one, or state that there is no common solution
(Short Answer)
4.9/5  (36)
(36)
A) Give an equation that is dependent with
B) Give an equation that is inconsistent wit
(Essay)
4.9/5  (34)
(34)
A racing chicken and a fast squirrel join Turtle and Rabbit in an over-and-back race, with known data as in the drawing below.  A) Going the same speed over and back, Rabbit just barely won the race. What was Rabbit's approximate speed? Explain your thinking.
B) Who came in second, third, and fourth? (Indicate ties, if any. No explanation is required.)
C) At the halfway mark of the race (300 feet), what was the order of the animals? (Indicate ties, if any. No explanation is required.)
D) What was Chicken's average speed over?
A) Going the same speed over and back, Rabbit just barely won the race. What was Rabbit's approximate speed? Explain your thinking.
B) Who came in second, third, and fourth? (Indicate ties, if any. No explanation is required.)
C) At the halfway mark of the race (300 feet), what was the order of the animals? (Indicate ties, if any. No explanation is required.)
D) What was Chicken's average speed over?
(Essay)
4.9/5  (44)
(44)
Use the substitution method to find a common solution to the given equations, if there is one, or state that there is no common solution.
(Essay)
4.8/5  (43)
(43)
One building has parallel elevator shafts for a passenger elevator P and a freight elevator F. Assume that each elevator moves at (its) steady speed and can start and stop instantly. One time during a particular day, P and F start trips at the same time. After 2 minutes, P was 400 feet from the bottom of the shafts, heading down, and F was 120 feet from the bottom, heading up at a speed of 20 feet/minute. Four minutes after the start of the trip, P was 280 feet from the bottom of the shafts.
A) Write an equation describing the height h of elevator P (in feet) above the bottom of the shafts, t minute(s) after the start of the trip.
B) At what height did elevator P start the trip, and what was its speed?
C) Write an equation describing the height h of elevator F (in feet) above the bottom of the shafts, t minute(s) after the start of the trip.
D) When the trips started, where was elevator F?
E) When, if ever, were the two elevators at the same height above the bottom of the shafts? If they were at the same height, what was that height?
(Essay)
4.9/5  (41)
(41)
A) Find a function rule that gives the perimeter (distance around the outside) of the n-module in the pattern below. (Use the shortest segment as the measuring unit.) Show your work. Simplify by collecting any like terms.
B) Justify that your rule in part A will always work.
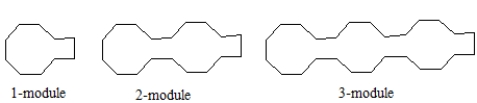
(Essay)
4.9/5  (29)
(29)
Use the addition/subtraction method to find a common solution to the given equations, if there is one, or state that there is no common solution.
(Short Answer)
4.8/5  (37)
(37)
Use the addition/subtraction method to find a common solution to the given equations, if there is one, or state that there is no common solution.
(Essay)
4.8/5  (35)
(35)
Showing 41 - 55 of 55
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)