Exam 13: Partial Differentiation
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Let g be a function of a single variable having continuous second order derivatives, and letu(x, y) = g(y + mx) , for some constant real number m. Determine all values of m such that u(x, y) satisfies the partial differential equation 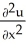 - 10
- 10 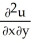 + 24
+ 24 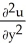 = 0.
= 0.
(Multiple Choice)
4.7/5  (31)
(31)
Describe the level curves of the function f(x,y) = 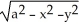 , where a > 0.
, where a > 0.
(Multiple Choice)
4.8/5  (42)
(42)
Find the equation of the normal line to the surface z = 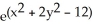 at the point(2, -2, 1).
at the point(2, -2, 1).
(Multiple Choice)
4.9/5  (45)
(45)
Assume that the relation 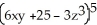 - 65 +
- 65 + 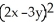 = 0 defines z as a differentiable functionof x and y near the point (x , y) = (4 , 0).
(a) If z = f(x , y) , find
= 0 defines z as a differentiable functionof x and y near the point (x , y) = (4 , 0).
(a) If z = f(x , y) , find 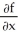 and
and 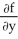 at (x,y) = (4 , 0).
(b) If x =
at (x,y) = (4 , 0).
(b) If x = 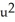 +
+ 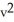 , y =
, y =  , find
, find 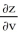 at (u , v) =(0 , 2)\.
Hints :Part (a): First , find the value of z at (x , y) =(4 , 0).
Part (b): Use the chain rule!
at (u , v) =(0 , 2)\.
Hints :Part (a): First , find the value of z at (x , y) =(4 , 0).
Part (b): Use the chain rule!
(Essay)
4.8/5  (40)
(40)
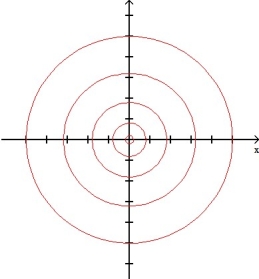
The graph below shows level curves f(x,y) = C for a function f and equally spaced values of C. Which of the following functions f is consistent with the graph?
(a) f(x,y) = 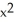 +
+ 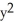 , (b) f(x,y) =
, (b) f(x,y) = 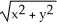 (c) f(x,y) =
(c) f(x,y) = 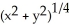
(Multiple Choice)
4.9/5  (33)
(33)
Find the two unit vectors tangent at the point (1, 1, 1) to the curve of intersection of the surfaces xy2 + x2y + z3 = 3 and x3 - y3 - xyz = -1.
(Multiple Choice)
4.8/5  (44)
(44)
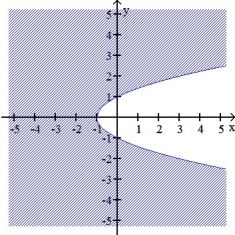
Identify the function f(x,y) whose domain is the shaded region shown in the figure below.
(Multiple Choice)
4.8/5  (32)
(32)
Find an equation of the plane tangent to the surface z = x2 - y2 at the point (2, 1, 3).
(Multiple Choice)
4.9/5  (41)
(41)
Assuming that the function f has continuous partial derivatives of orders 1 and 2, calculate and simplify 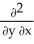 f(
f( 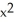 y, x
y, x 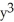 ).
).
(Multiple Choice)
4.9/5  (34)
(34)
Given that the relation y2 + y 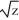 = 14 - sin(xz2) +
= 14 - sin(xz2) +  implicitly defines x as a differentiable function of y and z, find
implicitly defines x as a differentiable function of y and z, find 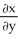 at the point (0, 3, 4).
at the point (0, 3, 4).
(Multiple Choice)
4.9/5  (45)
(45)
Find the slope of the tangent line to the curve that is the intersection of the surface z = x2 - y2 with the plane x = 2 at the point (2, 1, 3).
(Multiple Choice)
4.8/5  (49)
(49)
Find an equation of the plane tangent to the surface xy3z2 = 2 at the point (2, 1, -1).
(Multiple Choice)
5.0/5  (41)
(41)
Showing 41 - 60 of 104
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)