Exam 10: Sequences, Series, and Power Series
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
The interval of convergence of the power series 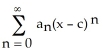 is given by [-7, -3).Find the centre c and the radius of convergence R of the power series.
is given by [-7, -3).Find the centre c and the radius of convergence R of the power series.
(Multiple Choice)
4.9/5  (41)
(41)
Find the Taylor series for f(x) = ln 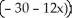 about c = - 3. Where does the series converge to f(x)?
about c = - 3. Where does the series converge to f(x)?
(Multiple Choice)
4.9/5  (47)
(47)
For exactly what values of the constant p does the series 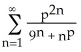 converge?
converge?
(Multiple Choice)
4.8/5  (42)
(42)
Find the Maclaurin series for ln 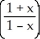 . For what values of x does the series converge to the function?
. For what values of x does the series converge to the function?
(Multiple Choice)
4.7/5  (32)
(32)
Let f(x) denote the sum of the series 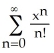 wherever the series converges. Where does the series converge? Calculate
wherever the series converges. Where does the series converge? Calculate  (x) and f(0). What do these results imply that f(x) actually is?
(x) and f(0). What do these results imply that f(x) actually is?
(Essay)
4.8/5  (43)
(43)
Determine all values of the constant real number k so that the Fourier series of the periodic function f(t) = 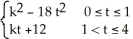 , f(t + 4) = f(t)
Converges to f(t) for all t
, f(t + 4) = f(t)
Converges to f(t) for all t  (- , ).
(- , ).
(Multiple Choice)
4.9/5  (34)
(34)
The sequence 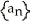 is defined recursively by
is defined recursively by 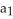 =
=  ,
, 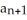 =
= 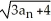 , n = 1, 2, 3,...Assuming the sequence converges to the real number L, find L.
, n = 1, 2, 3,...Assuming the sequence converges to the real number L, find L.
(Multiple Choice)
4.9/5  (31)
(31)
Showing 81 - 100 of 125
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)