Exam 14: Inference About Simple Regression
Exam 1: Statistics Success Stories and Cautionary Tales79 Questions
Exam 2: Turning Data Into Information94 Questions
Exam 3: Relationships Between Quantitative Variables99 Questions
Exam 4: Relationships Between Categorical Variables100 Questions
Exam 5: Sampling: Surveys and How to Ask Questions109 Questions
Exam 6: Gathering Useful Data for Examining Relationships90 Questions
Exam 7: Probability112 Questions
Exam 8: Random Variables115 Questions
Exam 9: Understanding Sampling Distributions: Statistics As Random Variables231 Questions
Exam 10: Estimating Proportions With Confidence104 Questions
Exam 11: Estimating Means With Confidence103 Questions
Exam 12: Testing Hypotheses About Proportions139 Questions
Exam 13: Testing Hypotheses About Means166 Questions
Exam 14: Inference About Simple Regression115 Questions
Exam 15: More About Inference for Categorical Variables111 Questions
Exam 16: Analysis of Variance111 Questions
Exam 17: Turning Information Into Wisdom70 Questions
Select questions type
Use the following information for questions:
Data has been obtained on the house size (in square feet) and the selling price (in dollars) for a sample of 100 homes in your town. Your friend is saving to buy a house and she asks you to investigate the relationship between house size and selling price and to develop a model to predict the price from size.
-What is the estimated change in the average selling price of a house for an increase in house size of 100 square feet?
(Short Answer)
4.8/5  (34)
(34)
Use the following information for questions:
A consumer agency employee has been researching and testing food products for months. He is convinced that the dimensions of the packaging used for dry goods (crackers, cookies, cereal, etc) all satisfy a certain ratio. He will try to model the relationship between the minimum width of a box and the height of the box, to see if he can predict the height of the box from the minimum width (both measured in inches). Data is collected on 24 randomly selected products. The scatterplot shows that a linear model is appropriate. (Partial) SPSS output is provided below.

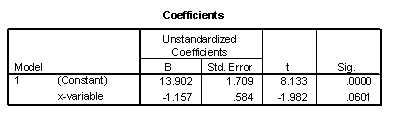 -What is the equation of the least squares regression line?
-What is the equation of the least squares regression line?
(Short Answer)
4.8/5  (29)
(29)
Use the following information for questions:
A regression line relating y =student's height (inches) to x = father's height (inches) for n = 70 college males is = 15 + 0.8 x.
-What is the estimated height of a son whose father's height is 70 inches?
(Short Answer)
4.8/5  (34)
(34)
Use the following information for questions:
A representative sample of n = 12 male college students is used to find a regression equation for y = weight (lbs) and x = height (inches). The least squares regression equation is = 30 + 2 x. The standard error of the estimated slope is 1. The following hypotheses will be tested:
H0:
Ha:
-What is the p-value for testing the following hypothesis about the correlation coefficient 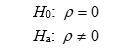
(Multiple Choice)
4.8/5  (28)
(28)
Use the following information for questions:
The data from a representative sample of 43 male college students was used to determine a regression equation for y = weight (lbs) and x = height (inches). The least squares regression equation was = -318 + 7.00 x. The error sum of squares (SSE) was 23617; the total sum of squares (SSTO) = 34894.
-What is the proportion of variation in weight that is explained by the linear relationship with height?
(Multiple Choice)
4.7/5  (36)
(36)
Consider the following plot of residuals versus x for a regression analysis. 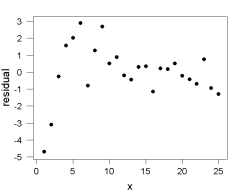 Which statement is not true about the regression model?
Which statement is not true about the regression model?
(Multiple Choice)
4.9/5  (37)
(37)
Use the following information for questions:
The heights (in inches) and foot lengths (in centimeters) of 32 college men were used to develop a model for the relationship between height and foot length. The scatterplot shows that a linear model is appropriate. SPSS output is provided below. 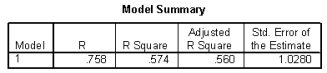
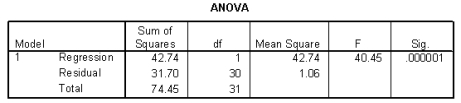
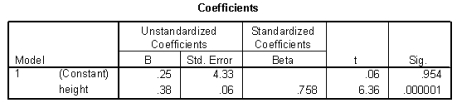 -Max is 70 inches tall. If a 95% prediction interval for his foot length were calculated, the width of this interval would _______ with respect to the interval from question 99.
-Max is 70 inches tall. If a 95% prediction interval for his foot length were calculated, the width of this interval would _______ with respect to the interval from question 99.
(Multiple Choice)
4.7/5  (25)
(25)
Use the following information for questions:
The heights (in inches) and foot lengths (in centimeters) of 32 college men were used to develop a model for the relationship between height and foot length. The scatterplot shows that a linear model is appropriate. SPSS output is provided below. 

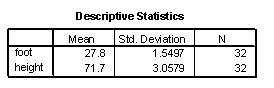
 -Calculate a 95% confidence interval for the average foot length for all college men who are 70 inches tall. Descriptive statistics for the two variables are provided below. Use the mean to obtain and note that
-Calculate a 95% confidence interval for the average foot length for all college men who are 70 inches tall. Descriptive statistics for the two variables are provided below. Use the mean to obtain and note that 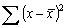 = 289.87
= 289.87
(Short Answer)
5.0/5  (36)
(36)
Shown below is a scatterplot of y versus x. 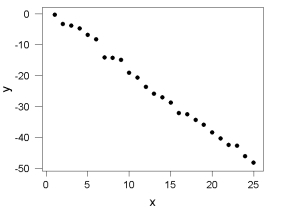 Which choice is most likely to be the approximate value of r2, the proportion of variation in y explained by the linear relationship with x?
Which choice is most likely to be the approximate value of r2, the proportion of variation in y explained by the linear relationship with x?
(Multiple Choice)
4.9/5  (27)
(27)
Use the following information for questions:
Data has been obtained on the house size (in square feet) and the selling price (in dollars) for a sample of 100 homes in your town. Your friend is saving to buy a house and she asks you to investigate the relationship between house size and selling price and to develop a model to predict the price from size.
-Identify the response and the explanatory variable.
(Short Answer)
4.8/5  (41)
(41)
Use the following information for questions:
A regression line relating y =grade point average to x = hours studied per week is estimated using data for n = 5 students. The estimated slope is b1 = 0.02. The standard error of the slope is s.e.(b1) = 0.01.
-What is a 95% confidence interval for 1 , the population slope ?
(Short Answer)
4.7/5  (23)
(23)
Use the following information for questions:
Data has been obtained on the house size (in square feet) and the selling price (in dollars) for a sample of 100 homes in your town. Your friend is saving to buy a house and she asks you to investigate the relationship between house size and selling price and to develop a model to predict the price from size.
-Some of the regression output is provided below.
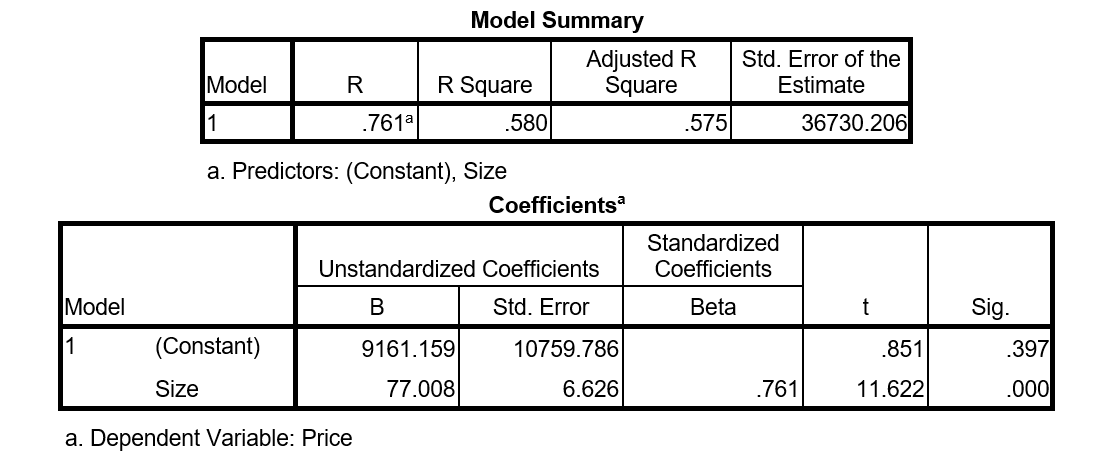 Give the value of and interpret it in the context of the problem.
Give the value of and interpret it in the context of the problem.
(Short Answer)
4.7/5  (30)
(30)
Use the following information for questions:
The heights (in inches) and foot lengths (in centimeters) of 32 college men were used to develop a model for the relationship between height and foot length. The scatterplot shows that a linear model is appropriate. SPSS output is provided below. 

 -What is the correlation between height and foot length?
-What is the correlation between height and foot length?
(Short Answer)
4.9/5  (38)
(38)
Use the following information for questions:
A regression line that relates y = hand span (cm) and x = height (inches) is = -1 + 0.3 x. The sample size was n = 5 adults. The standard deviation of the regression is s = 1 cm. For height = 60 inches, the standard error of the fit is s.e.(fit) = 1 cm.
-What is a 90% prediction interval for the hand span of a person whose height is 60 inches?
(Short Answer)
4.8/5  (37)
(37)
Use the following information for questions:
Data has been obtained on the house size (in square feet) and the selling price (in dollars) for a sample of 100 homes in your town. Your friend is saving to buy a house and she asks you to investigate the relationship between house size and selling price and to develop a model to predict the price from size.
-Give the least square regression equation for predicting price from house size.
(Short Answer)
4.9/5  (41)
(41)
Use the following information for questions:
A regression equation is determined that describes the relationship between average January temperature (degrees Fahrenheit) and geographic latitude, based on a random sample of cities in the United States. The equation is:
Temperature = 110 - 2(Latitude).
-Suppose that the latitudes of two cities differ by 10. What is the estimated difference in the average January temperatures in the two cities?
(Multiple Choice)
4.8/5  (30)
(30)
Use the following information for questions:
A regression equation is determined that describes the relationship between average January temperature (degrees Fahrenheit) and geographic latitude, based on a random sample of cities in the United States. The equation is:
Temperature = 110 - 2(Latitude).
-Estimate the average January temperature for a city at Latitude = 45.
(Multiple Choice)
4.9/5  (37)
(37)
Use the following information for questions:
Data has been obtained on the house size (in square feet) and the selling price (in dollars) for a sample of 100 homes in your town. Your friend is saving to buy a house and she asks you to investigate the relationship between house size and selling price and to develop a model to predict the price from size.
-Write the null and alternative hypotheses for assessing if there is a significant positive linear relationship between price and size for the population of all houses in your town.
(Short Answer)
4.8/5  (41)
(41)
Use the following information for questions:
The relation between y = ideal weight (lbs) and x =actual weight (lbs), based on data fromn = 119 women, resulted in the regression line = 44 + 0.60 x
-The slope of the regression line is ______
(Multiple Choice)
4.9/5  (41)
(41)
Use the following information for questions:
A car salesman is curious if he can predict the fuel efficiency of a car (in MPG) if he knows the fuel capacity of the car (in gallons). He collects data on a variety of makes and models of cars. The scatterplot shows that a linear model is appropriate. SPSS output is provided below.

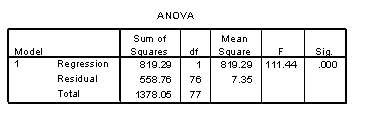
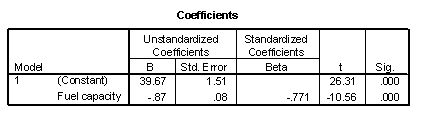 -How would the 95% confidence interval for the average fuel efficiency for all cars that hold 18 gallons of fuel compare to the interval calculated in question 89?
-How would the 95% confidence interval for the average fuel efficiency for all cars that hold 18 gallons of fuel compare to the interval calculated in question 89?
(Multiple Choice)
4.8/5  (36)
(36)
Showing 41 - 60 of 115
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)