Exam 14: Inference About Simple Regression

Use the following information for questions: A representative sample of 190 students resulted in a regression equation between y = left hand spans (cm) and x = right hand spans (cm). The least squares regression equation is $\hat{y}$ = 1.46 + 0.938 x. The error sum of squares (SSE) was 76.67, and total sum of squares (SSTO) was 784.8. -What is the value of r², the proportion of variation in left hand spans explained by the linear relationship with right hand spans.

Use the following information for questions: Can an athlete's cardiovascular fitness (as measured by time to exhaustion on a treadmill) help to predict the athlete's performance in a 20k ski race? To address this question the time to exhaustion on a treadmill (minutes) and the time to complete a 20k ski race (minutes) were recorded for a sample of 11 athletes. The researcher hypothesizes that there would be an inverse linear relationship, that is, the longer the time to exhaustion, the faster the athlete's time in the 20k ski race, on average. The data were used to provide the following output. 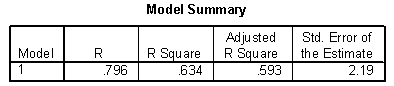-Based on this analysis, what percent of the variation in the ski race times is not accounted for by the linear regression between ski race time and time to exhaustion?

Use the following information for questions: A linear regression analysis of the relationship between y = daily hours of TV watched andx = age is done using data from n = 50 adults. The error sum of squares is SSE = 1,000. The total sum of squares is SSTO = 5,000. -What is the value of r², the proportion of variation in daily hours of TV watching explained by the linear relationship with x = age?

Use the following information for questions: A representative sample of 190 students resulted in a regression equation between y = left hand spans (cm) and x = right hand spans (cm). The least squares regression equation is $\hat{y}$ = 1.46 + 0.938 x. The error sum of squares (SSE) was 76.67, and total sum of squares (SSTO) was 784.8. -Use the empirical rule to find an interval that describes the left hand spans of approximately 95% of all individuals who have a right hand span of 26 cm.

Use the following information for questions: Data from a sample of 10 student is used to find a regression equation relating y = score on a 100-point exam to x = score on a 10-point quiz. The least squares regression equation is $\hat{y}$ = 35 + 6 x. The standard error of the slope is 2. The following hypotheses are tested: H₀: $β_1=0$ H_a: $β_1≠0$ -What is a 95% confidence interval for $\beta$ ₁ ? (Table A.2 or its equivalent needed.)

What is the best way to determine whether or not there is a statistically significant linear relationship between two quantitative variables?

Use the following information for questions: A representative sample of 190 students resulted in a regression equation between y = left hand spans (cm) and x = right hand spans (cm). The least squares regression equation is $\hat{y}$ = 1.46 + 0.938 x. The error sum of squares (SSE) was 76.67, and total sum of squares (SSTO) was 784.8. -For a student with a right and left hand span of 26 cm, what is the value of the residual?

Consider the following plot of residuals versus x for a regression analysis. 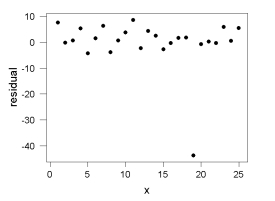Based on the plot, what problem with the regression model or data is most noticeable?

Use the following information for questions: Grades for a random sample of students who have taken statistics from a certain professor over the past 20 year were used to estimate the relationship between y = grade on the final exam and x = average exam score (for the three exams given during the term). 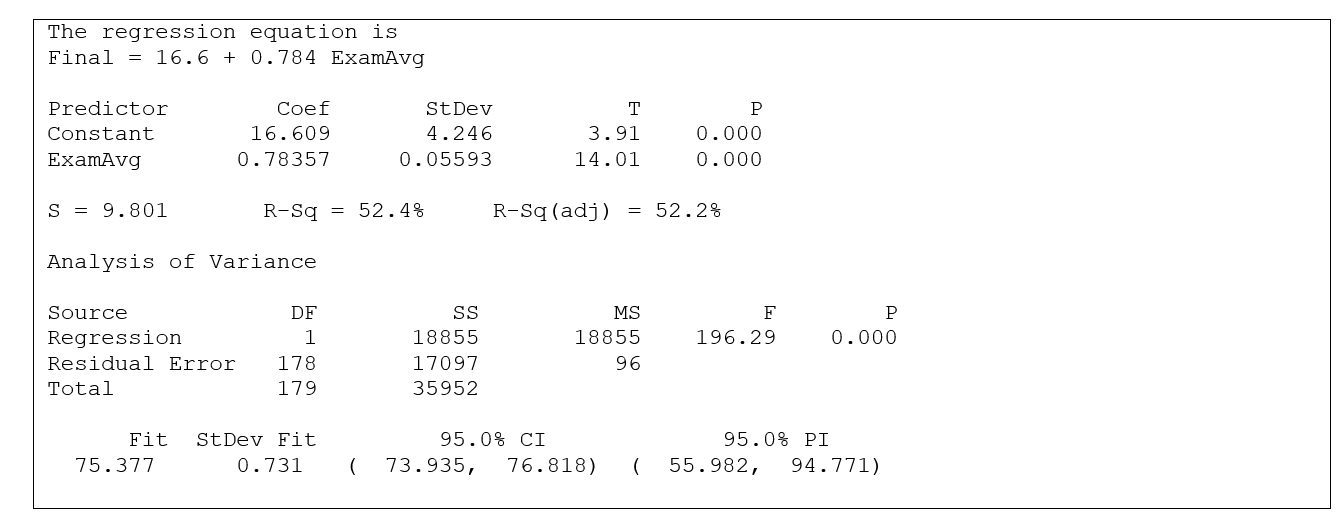-The estimate of the population standard deviation $\sigma$ is given by

Use the following information for questions: The relation between y = ideal weight (lbs) and x =actual weight (lbs), based on data fromn = 119 women, resulted in the regression line $\hat{y}$ = 44 + 0.60 x -If a woman weighs 120 pounds and her ideal weight is just that, 120 pounds, then her residual is

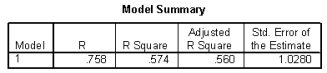
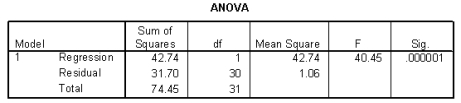
Use the following information for questions: The heights (in inches) and foot lengths (in centimeters) of 32 college men were used to develop a model for the relationship between height and foot length. The scatterplot shows that a linear model is appropriate. SPSS output is provided below. 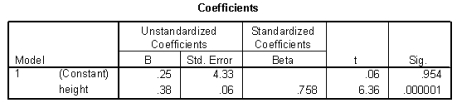-Based on this model, predict the difference in the foot lengths of college men whose heights different by 10 inches. Include the units.

A regression line is used for all of the following except one. Which one is not a valid use of a regression line?

Use the following information for questions: The heights (in inches) and foot lengths (in centimeters) of 32 college men were used to develop a model for the relationship between height and foot length. The scatterplot shows that a linear model is appropriate. SPSS output is provided below. -Suppose Max is 70 inches tall and has a foot length of 28.5 centimeters. Based on the least squares regression line, what is the value of the residual for Max?

Use the following information for questions: Data has been obtained on the house size (in square feet) and the selling price (in dollars) for a sample of 100 homes in your town. Your friend is saving to buy a house and she asks you to investigate the relationship between house size and selling price and to develop a model to predict the price from size. -Consider the scatterplot below. 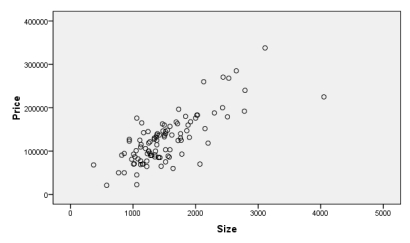Does a linear relationship between price and size seem reasonable? If so, what appears to be the direction of the relationship?

Use the following information for questions: The data from a representative sample of 43 male college students was used to determine a regression equation for y = weight (lbs) and x = height (inches). The least squares regression equation was $\hat{y}$ = -318 + 7.00 x. The error sum of squares (SSE) was 23617; the total sum of squares (SSTO) = 34894. -For a male student with a height of 70 inches and a weight of 200 lbs, what is the value of the residual?

Use the following information for questions: A linear regression analysis of the relationship between y = grade point average and x = hours studied per week is done using data from n = 10 students. The error sum of squares is SSE = 100 and the total sum of squares is SSTO = 900. -What is the value of s = estimated standard deviation for the regression?

Use the following information for questions: A sample of 19 female bears was measured for chest girth (y) and neck girth (x), both in inches. The least squares regression equation relating the two variables is $\hat{y}$ = 5.32 + 1.53 x. The standard deviation of the regression is s = 3.692. -What is a 95% confidence interval for the average (or mean) chest girth for bears with a neck girth of 20 inches? The standard error of the fit is s.e.(fit) = 0.880

What is the main distinction between a confidence interval and a prediction interval?

Use the following information for questions: The relation between y = ideal weight (lbs) and x =actual weight (lbs), based on data fromn = 119 women, resulted in the regression line $\hat{y}$ = 44 + 0.60 x -If a woman weighs 100 pounds and her ideal weight is just that, 100 pounds, then her residual is

Use the following information for questions: A sample of 19 female bears was measured for chest girth (y) and neck girth (x), both in inches. The least squares regression equation relating the two variables is $\hat{y}$ = 5.32 + 1.53 x. The standard deviation of the regression is s = 3.692. -What is a 95% prediction interval for the chest girth of a bear with a neck girth of 18 inches? The standard error of the fit, s.e.(fit), = 0.860