Exam 3: Relationships Between Quantitative Variables

A regression analysis done with Minitab for left foot length (y variable) and right foot length (x variable) for 55 college students gave the following output. The regression equation for left foot length (y variable) and right foot length (x variable) is

Use the following information for questions: A regression was done for 20 cities with latitude as the explanatory variable (x) and average January temperature as the response variable (y). The latitude is measured in degrees and average January temperature in degrees Fahrenheit. The latitudes ranged from 26 (Miami) to 47 (Duluth) The regression equation is $\hat{y}$ = 49.4 - 0.313x. -What is the value of the correlation coefficient r?

A researcher reports that the correlation between two quantitative variables is r = 0.8. Which of the following statements is correct?

Use the following information for questions: The 25 item "Parenting Hassles Scale" asks parents questions about certain situations in their family. They are asked to rate these situations on (1) how often they occur (frequency), and (2) how much they bother them (intensity). The score system for the frequency was 0-4 points (0 = never, 4 = all the time) and for the intensity 1-5 (1 = not much at all, 5 = very much). If an item received a 0 (zero) for frequency, it automatically received a 0 (zero) for intensity. The two variables, frequency and intensity, were formed by taking the total of the corresponding scores from the two rating scales across the various situations. In a scatterplot, these two variables showed an approximate linear relationship. They were then used to run a linear regression to predict intensity based on frequency. 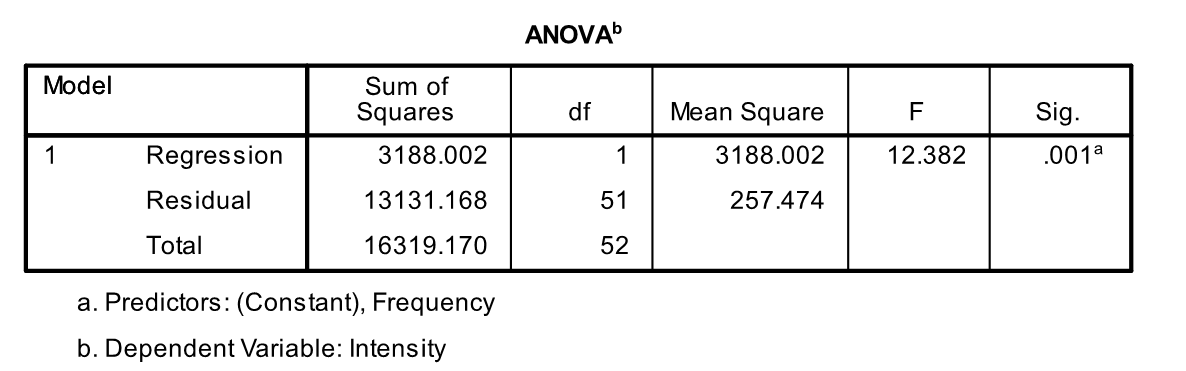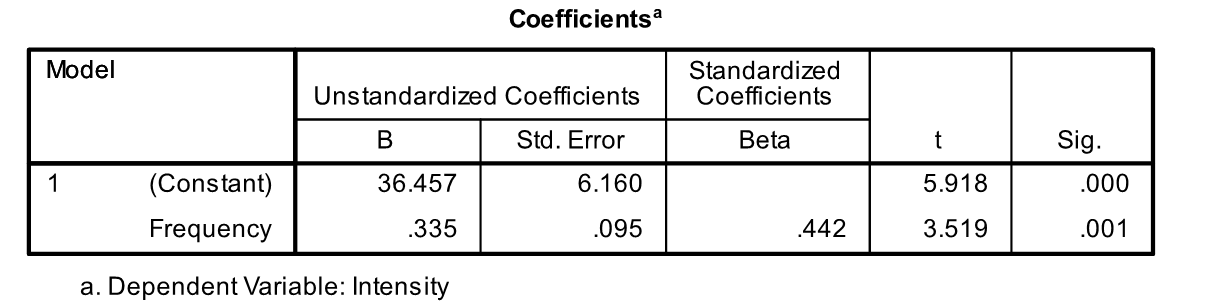-Dan filled out the "Parenting Hassles Scale". He scored 25 on the frequency scale and 41 on the intensity scale. What is the value of Dan's residual?

The correlation between father's heights and student's heights for a sample of 79 male students is r = 0.669. What is the proportion of variation in son's heights explained by the linear relationship with father's heights?

A scatterplot of the self-reported weights (y variable) and self-reported heights (x variable) for 176 college students follows. 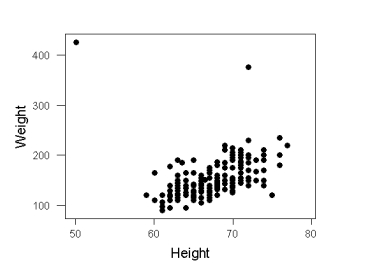What is the main difficulty with using a regression line to analyze these data?

Use the following information for questions: The next three questions are based on a regression equation for 55 college students with x = left forearm length (cm) and y = height. The forearm lengths ranged from 22 cm to 31 cm. The regression equation is $\hat{y}$ = 30.3 + 1.49x -One student's left forearm length was 22 cm, and her height was 63 inches. What is the estimated height for this student, based on the regression equation? What is the residual?

For which one of these relationships could we use a regression analysis? Only one choice is correct.

Use the following information for questions: A regression was done for 20 cities with latitude as the explanatory variable (x) and average January temperature as the response variable (y). The latitude is measured in degrees and average January temperature in degrees Fahrenheit. The latitudes ranged from 26 (Miami) to 47 (Duluth) The regression equation is $\hat{y}$ = 49.4 - 0.313x -The city of Miami, Florida has latitude 26 degrees with average January temperature of 67 degrees Fahrenheit. What is the estimated average January temperature for Miami, based on the regression equation? What is the residual?

Use the following information for questions: Past data has shown that the regression line relating the final exam score and the midterm exam score for students who take statistics from a certain professor is: final exam = 50 + 0.5 * midterm -What is the predicted final exam score for a student with a midterm score of 50?

Two variables have a positive association when

Which one of the following is not appropriate for studying the relationship between two quantitative variables?

Use the following information for questions: Consider the following scatterplots for two quantitative variables y and x. One point has been labeled in each plot. 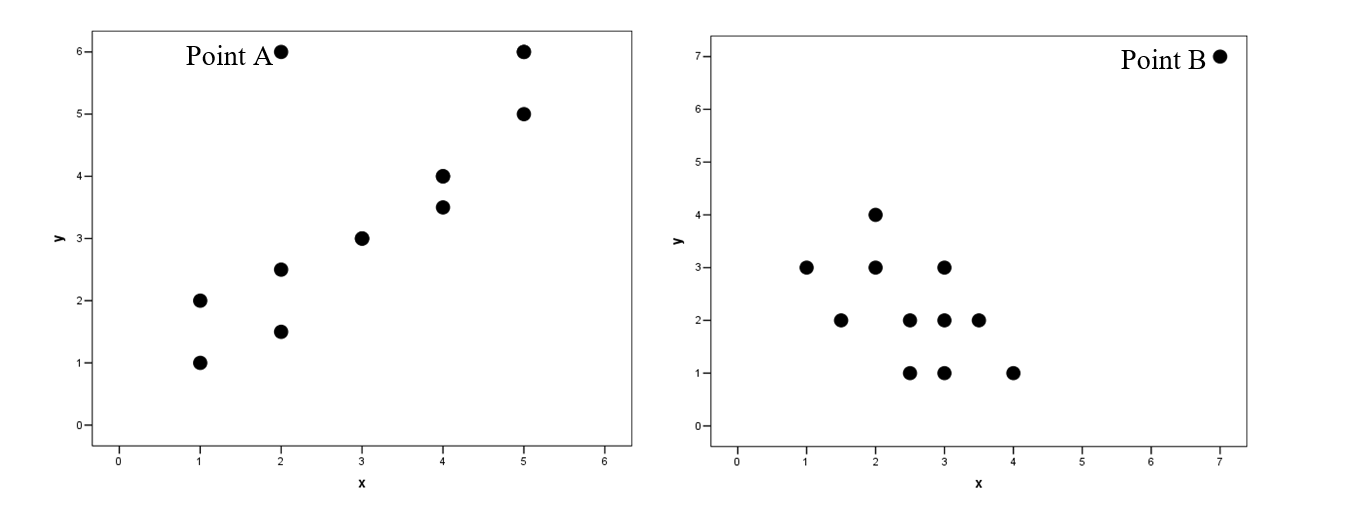-Which point would be the most influential?

A professor found a negative correlation between the number of hours students came to her office hours and their score on her final exam. What possible confounding variable could explain the observed negative correlation?

Which of the following correlation values indicates the strongest linear relationship between two quantitative variables?

A researcher would like to study the relationship between y = graduating GPA of students at a university and x = major field of study (1 = science, 2 = humanities, etc.). What is a possible difficulty with using a regression line to analyze these data?

A scatterplot of the price of a book (y variable) versus the number of pages in the book (x variable) is shown for 15 books in a professors office. In addition, the symbol "o" shows that the book was a hardcover book, while the symbol "+" shows that the book was a softcover book. 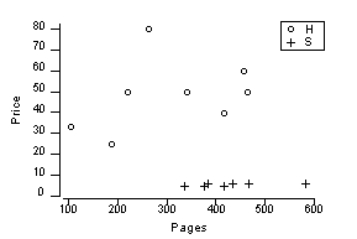What is the main difficulty with using a regression line to analyze these data?

Use the following information for questions: Past data has shown that the regression line relating the final exam score and the midterm exam score for students who take statistics from a certain professor is: final exam = 50 + 0.5 * midterm -Which of the following gives a correct interpretation of the intercept?

Which one of the following cannot be determined from a scatterplot?

A regression line can be used to predict the unknown value of x for an individual, given that individual's y value.