Exam 8: Sets and Probability
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Solve the problem, rounding the answer as appropriate. Assume that "pure dominant" describes one who has twodominant genes for a given trait; "pure recessive" describes one who has two recessive genes for a given trait; and"hybrid" describes one who has one of each.
-Suppose a hybrid mates with a pure dominant. If they produce two offspring, what is the probability that neither is a hybrid?
(Multiple Choice)
4.9/5  (35)
(35)
Let and . List the members of the indicated set, using set braces.
-
(Multiple Choice)
4.7/5  (41)
(41)
Determine whether the given events are disjoint.
-Being over 30 and being in college
(True/False)
4.8/5  (44)
(44)
The table shows, for some particular year, a listing of several income levels and, for each level, the proportion of the population in the level and the probability that a person in that level bought a new car during the year. Given that one of the people who bought a new car during that year is randomly selected, find the probability that that person was in the indicated income category. Round your answer to the nearest hundredth.
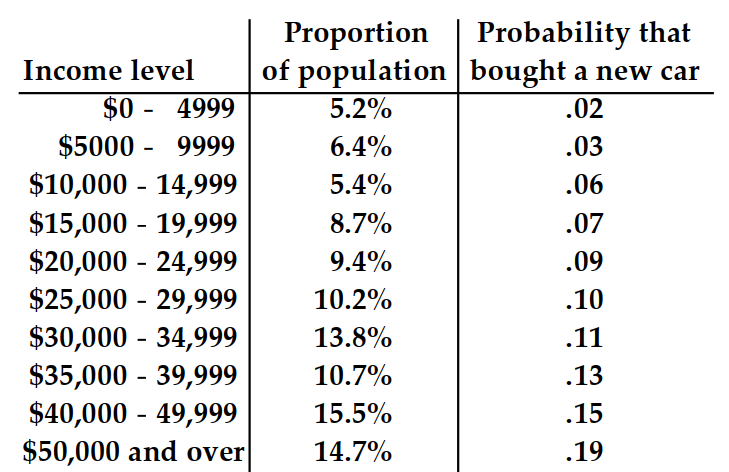 -
-
(Multiple Choice)
4.8/5  (44)
(44)
Write the sample space for the given experiment.
-A lottery uses balls numbered 1 through 39. An even-numbered ball is picked.
(Multiple Choice)
4.8/5  (41)
(41)
A sample space is a set of 7 outcomes. What is the most distinct events that can have?
(Multiple Choice)
4.7/5  (46)
(46)
Let and . List the members of the indicated set, using set braces.
-B'
(Multiple Choice)
4.8/5  (39)
(39)
Decide whether the two events listed are independent.
-Two cards are selected, without replacement, from an ordinary deck. F is the event that an ace appears on the first draw. is the event that an ace appears on the second draw.
(True/False)
4.8/5  (39)
(39)
Assume that and are events. Must the union of and also be an event? Must the intersection of and also be an event?
(Multiple Choice)
4.8/5  (38)
(38)
An experiment is conducted for which the sample space is assignment ispossible for this experiment.
-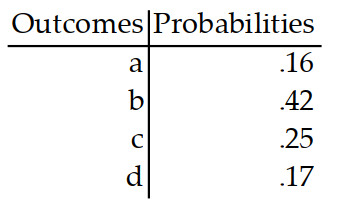
(True/False)
4.9/5  (37)
(37)
Use a Venn diagram to decide if the statement is true or false.
-
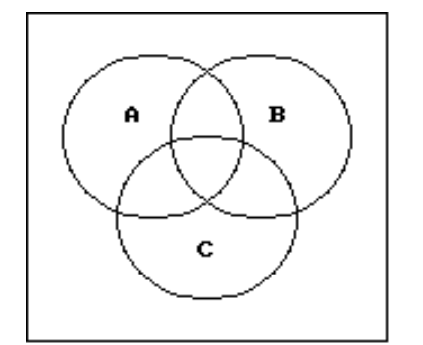
(True/False)
4.8/5  (36)
(36)
Write the sample space for the given experiment.
-An ordinary die is rolled.
(Multiple Choice)
5.0/5  (40)
(40)
The table shows, for some particular year, a listing of several income levels and, for each level, the proportion of the population in the level and the probability that a person in that level bought a new car during the year. Given that one of the people who bought a new car during that year is randomly selected, find the probability that that person was in the indicated income category. Round your answer to the nearest hundredth.
 - -
- -
(Multiple Choice)
4.9/5  (35)
(35)
Suppose P(C) = .048, P(M ꓵ C) = .044, and P(M ꓴ C) = .524. Find the indicated probability.
-
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-Below is a table of data from a high school survey given to 500 parents. Find the probability that a rand omly chosen parent would agree or strongly agree that the school is clean. Round your answer to the nearest hundred th.
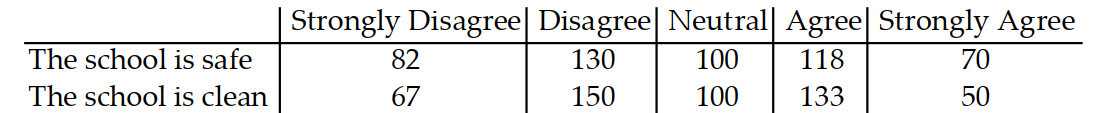
(Multiple Choice)
4.9/5  (43)
(43)
Let be the smallest possible universal set that includes all of the crops listed; and let , and be the sets of five crops in Alabama, Arkansas, and Louisiana, respectively. Find the indicated set.
-
(Multiple Choice)
4.8/5  (30)
(30)
Solve the problem.
-The given contingency table gives the number (in thousands) of U.S. households classified by educational attainment (high school graduate or less denoted with A, some college with no degree denoted B, an associate's degree denoted with C, and a bachelor's degree or higher denoted with D) and household income ($0 - $34,999 denoted with E, $35,000-$49,999 denoted with F,$50,000-$74,999 denoted G, and $75,000 and over denoted H).
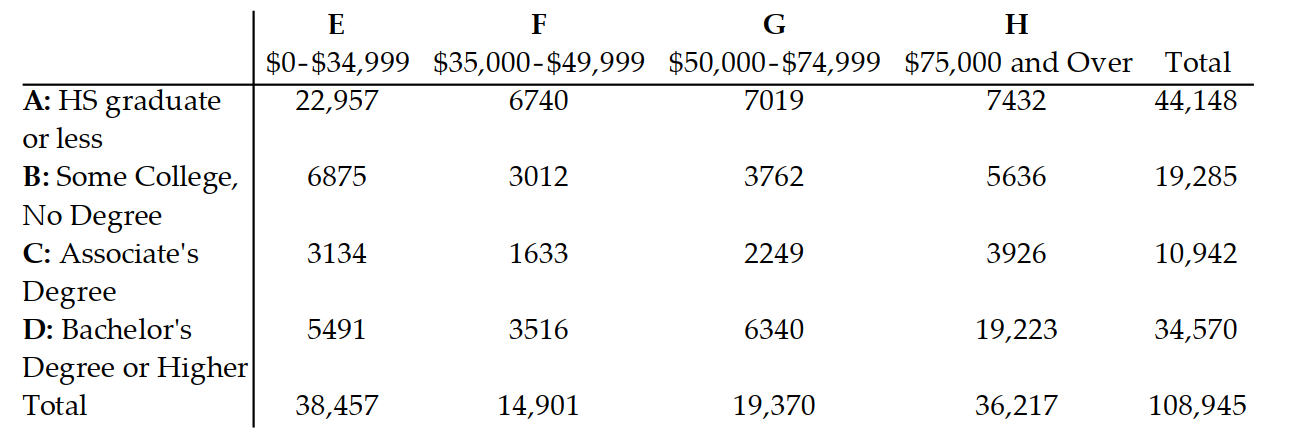 Find the number of households in the given set.
Find the number of households in the given set.
(Multiple Choice)
4.9/5  (41)
(41)
Find the probability of the given event.
-A bag contains 7 red marbles, 3 blue marbles, and 1 green marble. A randomly drawn marble is not blue.
(Multiple Choice)
4.8/5  (38)
(38)
An experiment is conducted for which the sample space is assignment ispossible for this experiment.
-
(True/False)
4.9/5  (34)
(34)
Showing 201 - 220 of 240
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)