Exam 8: Sets and Probability
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Solve the problem.
-A survey revealed that of people are entertained by reading books, are entertained by watching TV, and are entertained by both books and TV. What is the probability that a person will be entertained by either books or TV? Express the answer as a percentage.
(Multiple Choice)
4.9/5  (29)
(29)
Write the sample space for the given experiment.
-A box contains 3 blue cards numbered 1 through 3 , and 4 green cards numbered 1 through 4 . A blue card is picked, followed by a green card.
(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-If two fair dice are rolled, find the probability that the roll is a double given that the sum is 11 .
(Multiple Choice)
4.9/5  (30)
(30)
Let be the smallest possible universal set that includes all of the crops listed; and let , and be the sets of five crops in Alabama, Arkansas, and Louisiana, respectively. Find the indicated set.
-
(Multiple Choice)
4.9/5  (38)
(38)
Tell whether the statement is true or false.
- is an even counting number
(True/False)
4.8/5  (35)
(35)
Find the probability.
-A family has five children. The probability of having a girl is . What is the probability of having at least 4 girls? Round the answer to the fourth decimal place.
(Multiple Choice)
4.9/5  (36)
(36)
Use a Venn diagram to decide if the statement is true or false.
-
(True/False)
4.7/5  (39)
(39)
Insert " " or "q" in the blank to make the statement true.
-
(Multiple Choice)
4.8/5  (43)
(43)
Use a Venn diagram to answer the question.
-At East Zone University (EZU) there are 688 students taking College Algebra or Calculus. 495 are taking College Algebra, 210 are taking Calculus, and 17 are taking both College Algebra and Calculus. How many are taking Calculus but not Algebra?
(Multiple Choice)
4.8/5  (31)
(31)
Find the probability.
-A family has five children. The probability of having a girl is . What is the probability of having 2 girls followed by 3 boys? Round the answer to the fourth decimal place.
(Multiple Choice)
4.9/5  (43)
(43)
Determine whether the given events are disjoint.
-Drawing a spade from a deck of cards and drawing an ace
(True/False)
4.9/5  (33)
(33)
A die is rolled twice. Write the indicated event in set notation.
-The sum of the rolls is 8.
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-Of the coffee makers sold in an appliance store, have either a faulty switch or a defective cord, have a faulty switch, and have both defects. What is the probability that a coffee maker will have a defective cord? Express the answer as a percentage.
(Multiple Choice)
4.9/5  (35)
(35)
Let be the smallest possible universal set that includes all of the crops listed; and let , and be the sets of five crops in Alabama, Arkansas, and Louisiana, respectively. Find the indicated set.
-
(Multiple Choice)
4.9/5  (36)
(36)
The table shows, for some particular year, a listing of several income levels and, for each level, the proportion of the population in the level and the probability that a person in that level bought a new car during the year. Given that one of the people who bought a new car during that year is randomly selected, find the probability that that person was in the indicated income category. Round your answer to the nearest hundredth.
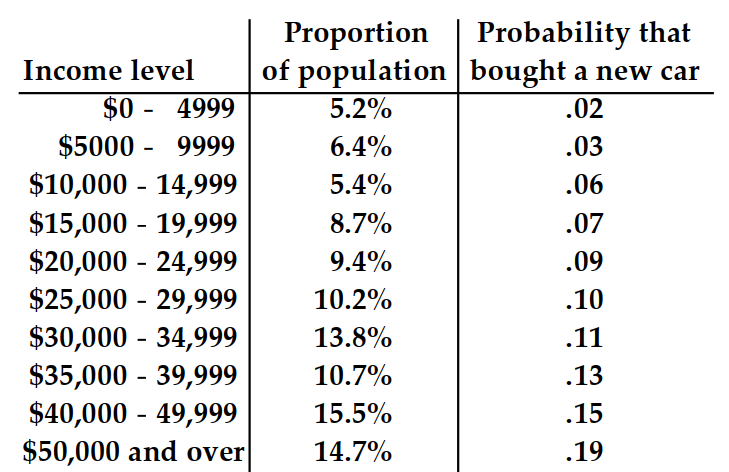 - -
- -
(Multiple Choice)
4.7/5  (35)
(35)
Solve the problem using Bayes' Theorem. Round the answer to the nearest hundredth, if necessary.
-For mutually exclusive events , and , let , and . Also, and . Find .
(Multiple Choice)
4.9/5  (39)
(39)
Find the probability.
-In a certain city, of the people are business executives, and of the business executives drive Cadillacs. Assuming independent events, what is the probability of choosing a business executive who drives a Cadillac? Round the answer to the nearest hundredth.
(Multiple Choice)
4.9/5  (32)
(32)
For the experiment described, write the indicated event in set notation.
-From six job applicants, two people are selected for an interview. The names of the applicants are Ruth, Kim, Nancy, Jeff, Mark, and Lisa. Represent the event "Lisa is selected" as a subset of the sample space.
(Multiple Choice)
5.0/5  (29)
(29)
Showing 61 - 80 of 240
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)