Exam 8: Sets and Probability

Solve the problem. Express the answer as a percentage. -37\% of the workers at Motor Works are female, while $70 \%$ of the workers at City Bank are female. If one of these companies is selected at random (assume a 50-50 chance for each), and then a worker is selected at random, what is the probability that the worker will be female?

Find the odds in favor of the indicated event. -Randomly drawing a number greater than 2 from the cards pictured below.

Shade the Venn diagram to represent the set. - $\left(A \cup B \cup C^{\prime}\right)^{\prime}$

Solve the problem using Bayes' Theorem. Round the answer to the nearest hundredth, if necessary. -For mutually exclusive events $X_{1}, X_{2}$ , and $X_{3}$ , let $P\left(X_{1}\right)=.15, P\left(X_{2}\right)=.64$ , and $P\left(X_{3}\right)=.21$ . Also, $\mathrm{P}\left(\mathrm{Y} \mid \mathrm{X}_{1}\right)=.40, \mathrm{P}\left(\mathrm{Y} \mid \mathrm{X}_{2}\right)=.30$ , and $\mathrm{P}\left(\mathrm{Y} \mid \mathrm{X}_{3}\right)=.60$ . Find $\mathrm{P}\left(\mathrm{X}_{1} \mid \mathrm{Y}\right)$ .

Can $\mathrm{P}(\mathrm{A} \mid \mathrm{B})=\mathrm{P}(\mathrm{B} \mid \mathrm{A})$ if $\mathrm{A}$ and $\mathrm{B}$ are different?

Let $U=\{q, r, s, t, u, v, w, x, y, z\} ; A=\{q, s, u, w, y\} ; B=\{q, s, y, z\} ;$ and $C=\{v, w, x, y, z\}$ . List the members of the indicated set, using set braces. - $A \cap B^{\prime}$

Solve the problem. -The given contingency table gives the number (in thousands) of U.S. households classified by educational attainment (high school graduate or less denoted with $\mathrm{A}$ , some college with no degree denoted B, an associate's degree denoted with $C$ , and a bachelor's degree or higher denoted with D) and household income ( $ 0 - $34,999 denoted with E, $35,000-$49,999 denoted with F, $50,000-$74,999 denoted G, and $ 75,000 and over denoted H). 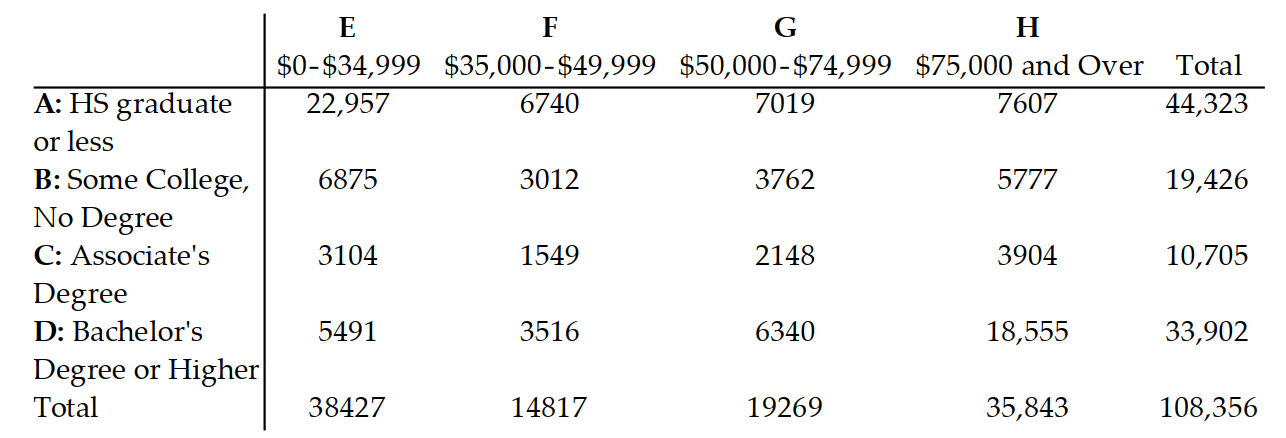Find the number of households in the given set. $(\mathrm{C} \cup \mathrm{D}) \cap \mathrm{H}$

Find the odds in favor of the indicated event. -Randomly drawing an even number from the cards pictured below.

Provide an appropriate response. -To find $\mathrm{P}(\mathrm{A} \mid \mathrm{B})$ using Bayes' theorem, what conditional probability occurs in the numerator?

Shade the Venn diagram to represent the set. - $\mathrm{A} \cup\left(\mathrm{B} \cap \mathrm{C}^{\prime}\right)$

A die is rolled twice. Write the indicated event in set notation. -The sum of the rolls is 5.

Write the sample space for the given experiment. -A box contains 10 red cards numbered 1 through 10. One card is drawn at random.

An experiment is conducted for which the sample space is $S$ assignment ispossible for this experiment. -

A die is rolled twice. Write the indicated event in set notation. -The second roll is a 3.

Shade the Venn diagram to represent the set. - $\mathrm{B} \cup\left(\mathrm{A} \cap \mathrm{C}^{\prime}\right)$

For the experiment described, write the indicated event in set notation. -A die is tossed twice with the tosses recorded as an ordered pair. Represent the following event as a subset of the sample space: The sum of the tosses is either three or four.

Use a Venn Diagram and the given information to determine the number of elements in the indicated set. - $n(U)=60, n(A)=29, n(B)=17$ , and $n(A \cap B)=3$ . Find $n(A \cup B)^{\prime}$ .

Provide an appropriate response. -Is $\mathrm{P}\left(\mathrm{R}^{\prime} \mid \mathrm{T}\right)=\frac{\mathrm{P}\left(\mathrm{R}^{\prime}\right) \cdot \mathrm{P}\left(\mathrm{T} \mid \mathrm{R}^{\prime}\right)}{\mathrm{P}(\mathrm{R}) \cdot \mathrm{P}(\mathrm{T} \mid \mathrm{R})+\mathrm{P}\left(\mathrm{R}^{\prime}\right) \cdot \mathrm{P}\left(\mathrm{T} \mid \mathrm{R}^{\prime}\right)}$ a valid alternative form of Bayes' theorem (special case)?

Use the given table to find the indicated probability. -The following table contains data from a study of two airlines which fly to Smalltown, USA. 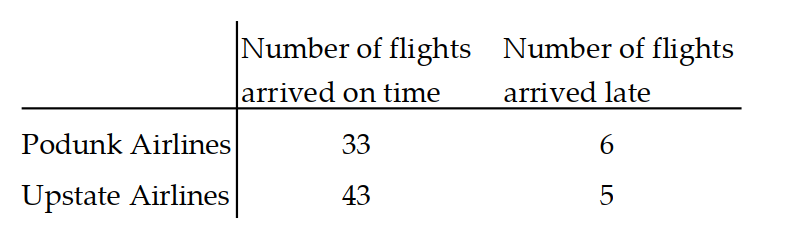P(flight arrived on time | flight was on Upstate Airlines)?

Solve the problem. Express the answer as a percentage. -A coin is biased to show $37 \%$ heads and $63 \%$ tails. The coin is tossed twice. What is the probability that the coin turns up heads on the second toss?