Exam 8: Sets and Probability
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Find the probability.
-A calculator requires a keystroke assembly and a logic circuit. Assume that of the keystroke assemblies and of the logic circuits are satisfactory. Find the probability that a finished calculator will be satisfactory.
(Multiple Choice)
5.0/5  (40)
(40)
Solve the problem, rounding the answer as appropriate. Assume that "pure dominant" describes one who has twodominant genes for a given trait; "pure recessive" describes one who has two recessive genes for a given trait; and"hybrid" describes one who has one of each.
-Two hybrids produce a litter of four offspring. What is the probability that exactly one is pure recessive?
(Multiple Choice)
4.8/5  (35)
(35)
Use the given table to find the indicated probability.
-People were given three choices of soft drinks and asked to choose one favorite. The following table shows the results.
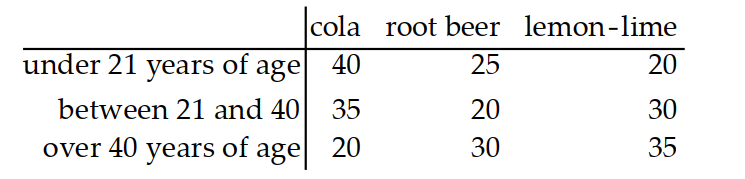 person is over 40 | person drinks root beer)?
person is over 40 | person drinks root beer)?
(Multiple Choice)
4.9/5  (33)
(33)
Use a Venn diagram to decide if the statement is true or false.
-
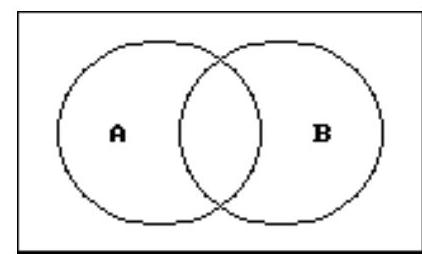
(True/False)
4.8/5  (40)
(40)
Write the word or phrase that best completes each statement or answers thequestion.
-If , why must ?
(Essay)
4.8/5  (35)
(35)
Let be the smallest possible universal set that includes all of the crops listed; and let , and be the sets of five crops in Alabama, Arkansas, and Louisiana, respectively. Find the indicated set.
-
(Multiple Choice)
4.9/5  (32)
(32)
A die is rolled twice. Write the indicated event in set notation.
-The first roll is a 2 and so is the second.
(Multiple Choice)
4.8/5  (32)
(32)
Let and . List the members of the indicated set, using set braces.
-
(Multiple Choice)
4.8/5  (35)
(35)
Find the odds in favor of the indicated event.
-Randomly drawing a 4 from the cards pictured below.

(Multiple Choice)
4.8/5  (35)
(35)
Use the given table to find the indicated probability.
-The following table contains data from a study of two airlines which fly to Smalltown, USA.
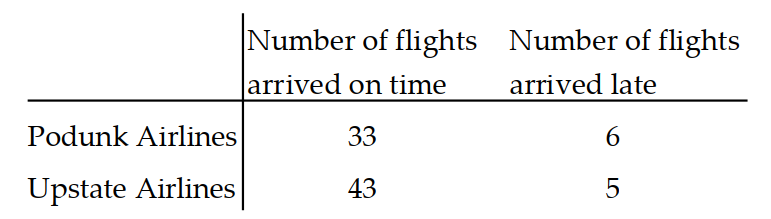 P(flight arrived on time flight was on Upstate Airlines)?
P(flight arrived on time flight was on Upstate Airlines)?
(Multiple Choice)
4.9/5  (37)
(37)
Decide whether the two events listed are independent.
-A fair die is rolled twice. F is the event that six appears on the first roll and is the event that six appears on the second roll.
(True/False)
4.8/5  (43)
(43)
Find the odds in favor of the indicated event.
-Rolling a 4 with a fair die.
(Multiple Choice)
4.8/5  (40)
(40)
Let be the smallest possible universal set that includes all of the crops listed; and let , and be the sets of five crops in Alabama, Arkansas, and Louisiana, respectively. Find the indicated set.
-
(Multiple Choice)
4.9/5  (36)
(36)
Use a Venn Diagram and the given information to determine the number of elements in the indicated set.
- , , and . Find .
(Multiple Choice)
4.8/5  (29)
(29)
Solve the problem, rounding the answer as appropriate. Assume that "pure dominant" describes one who has twodominant genes for a given trait; "pure recessive" describes one who has two recessive genes for a given trait; and"hybrid" describes one who has one of each.
-In a population, of females are pure dominant, are hybrid, and are pure recessive. If a pure recessive male mates with a random female and their first offspring has the dominant trait, what is the probability that the female is pure dominant?
(Multiple Choice)
4.8/5  (36)
(36)
The table shows, for some particular year, a listing of several income levels and, for each level, the proportion of the population in the level and the probability that a person in that level bought a new car during the year. Given that one of the people who bought a new car during that year is randomly selected, find the probability that that person was in the indicated income category. Round your answer to the nearest hundredth.
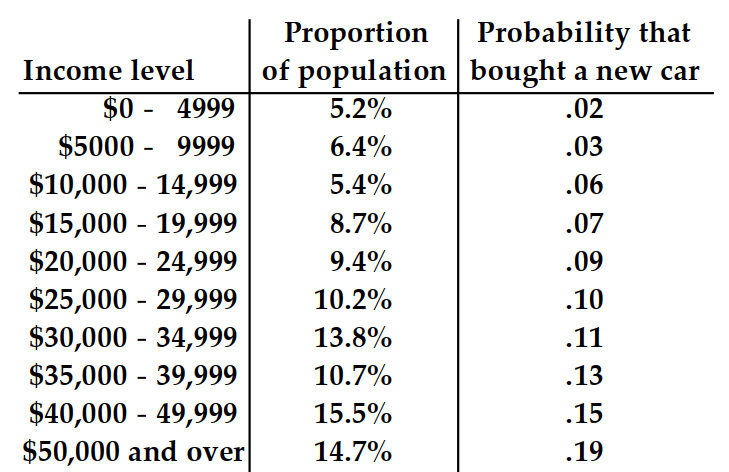 - -
- -
(Multiple Choice)
4.9/5  (35)
(35)
Write the word or phrase that best completes each statement or answers the question.
-Assume that the events are mutually exclusive events whose union is the sample space, and that is an event that has occurred. Use Bayes' theorem to write an equation for .
(Essay)
4.7/5  (43)
(43)
Use a Venn Diagram and the given information to determine the number of elements in the indicated set.
- , , and . Find
(Multiple Choice)
4.8/5  (32)
(32)
Showing 21 - 40 of 240
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)