Exam 8: Sets and Probability
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Write the sample space for the given experiment.
-A group of 12 people are assigned numbers 1 through 12. A person assigned a number of 5 or less is chosen.
(Multiple Choice)
5.0/5  (33)
(33)
The table shows, for some particular year, a listing of several income levels and, for each level, the proportion of the population in the level and the probability that a person in that level bought a new car during the year. Given that one of the people who bought a new car during that year is randomly selected, find the probability that that person was in the indicated income category. Round your answer to the nearest hundredth.
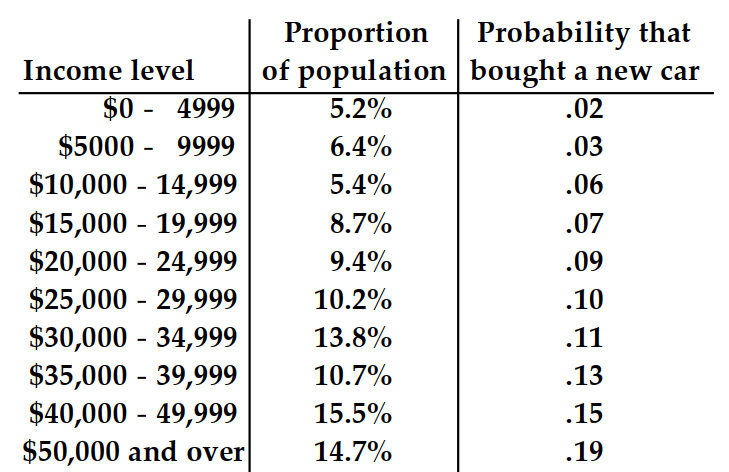 -
-
(Multiple Choice)
4.8/5  (41)
(41)
Find the number of subsets of the set.
- is an even number between 15 and 35
(Multiple Choice)
4.8/5  (30)
(30)
Suppose P(C) = .048, P(M ꓵ C) = .044, and P(M ꓴ C) = .524. Find the indicated probability.
-
(Multiple Choice)
4.9/5  (36)
(36)
Find the probability.
-A basketball player hits her shot of the time. If she takes four shots during a game, what is the probability that she misses the first shot and hits the last three? Express the answer as a percentage, and round to the nearest tenth (if necessary).
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem. Express the answer as a percentage.
-A coin is biased to show heads and tails. The coin is tossed twice. What is the probability that the coin turns up tails on both tosses?
(Multiple Choice)
4.7/5  (37)
(37)
Use a Venn Diagram and the given information to determine the number of elements in the indicated set.
- , and . Find .
(Multiple Choice)
4.7/5  (32)
(32)
Assume that, at a certain college, of all physics majors belong to ethnic minorities. Given a random sample of 10physics majors, find the probability of the indicated event. Round your answer as appropriate.
-On ly the first 2 belong to an ethnic minority.
(Multiple Choice)
4.8/5  (41)
(41)
Use the given table to find the indicated probability.
-College students were given three choices of pizza toppings and asked to choose one favorite. The following table shows the results.
 favorite topping is veggie student is junior or senior)?
Round the answer to the nearest hundredth.
favorite topping is veggie student is junior or senior)?
Round the answer to the nearest hundredth.
(Multiple Choice)
4.9/5  (37)
(37)
Assume that, at a certain college, of all physics majors belong to ethnic minorities. Given a random sample of 10physics majors, find the probability of the indicated event. Round your answer as appropriate.
-No more than 6 belong to an ethnic minority.
(Multiple Choice)
4.8/5  (35)
(35)
Use the given table to find the indicated probability.
-People were given three choices of soft drinks and asked to choose one favorite. The following table shows the results.
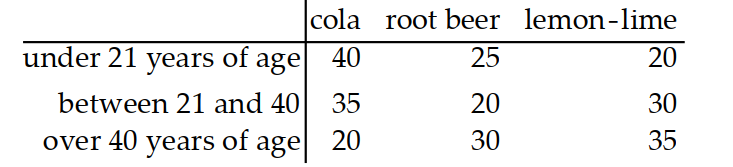 person drinks root beer person is over 40 ?
person drinks root beer person is over 40 ?
(Multiple Choice)
4.8/5  (33)
(33)
A sample space is a set of 6 outcomes. What is the least number of outcomes that an event defined for can have?
(Multiple Choice)
4.8/5  (39)
(39)
Use a Venn diagram to decide if the statement is true or false.
-
(True/False)
4.8/5  (33)
(33)
Solve the problem.
-One card is selected from a deck of cards. Find the probability of selecting a diamond or a card less than 6. (Note: The ace is considered a low card.)
(Multiple Choice)
4.9/5  (37)
(37)
Find the probability of the given event.
-A bag contains 4 red marbles, 6 blue marbles, and 9 green marbles. A randomly drawn marble is blue.
(Multiple Choice)
4.8/5  (43)
(43)
Use a Venn diagram to decide if the statement is true or false.
-
(True/False)
4.8/5  (29)
(29)
For the experiment described, write the indicated event in set notation.
-A die is tossed twice with the tosses recorded as an ordered pair. Represent the following event as a subset of the sample space: The first toss shows a one.
(Multiple Choice)
4.8/5  (37)
(37)
Decide whether the two events listed are independent.
-A fair die is rolled twice. is the event that the sum of the two rolls is eight and is the event that three appears on the first roll.
(True/False)
4.9/5  (31)
(31)
Solve the problem.
-Among 170 households surveyed, 58 have a video camera, 56 have a snapshot camera, 21 have binoculars, 4 have a video camera and a snapshot camera, 8 have a snapshot camera and binoculars, and 2 have all three products. What is the probability that a household will have a snapshot camera or binoculars? Express the answer as a fraction.
(Multiple Choice)
4.8/5  (35)
(35)
Showing 181 - 200 of 240
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)