Exam 7: Random Variables and Discrete Probability Distributions

Number of Hamsters The joint probability distribution of X and Y is shown in the accompanying table,where X denotes the number of hamsters that Quinn may have next year,and Y denotes the number of hamsters that her boyfriend,Jason,may have when she moves in with him next year. ​ ​ -{Number of Hamsters Narrative} Compute the covariance and the coefficient of correlation.

The amount of milk consumed by a baby in a day is an example of a discrete random variable.

Number of Hamsters The joint probability distribution of X and Y is shown in the accompanying table,where X denotes the number of hamsters that Quinn may have next year,and Y denotes the number of hamsters that her boyfriend,Jason,may have when she moves in with him next year. ​ ​ -{Number of Hamsters Narrative} Are X and Y independent? Explain.

Katie's Portfolio ​ Katie is given the following information about the returns on two stocks: E(R₁)= 0.10,E(R₂)= 0.15,V(R₁)= 0.0225,and V(R₂)= 0.0441. ​ ​ -{Katie's Portfolio Narrative} Compute the variance of the portfolio composed of 30% stock 1 and 70% stock 2,if the coefficient of correlation is 0.40.

A binomial experiment consists of a(n)____________________ number of trials,n.

One requirement of bivariate distributions is that .

Golfing Store The joint probability distribution of variables X and Y is shown in the table below,where X is the number of drivers and Y is the number of putters sold daily in a small golfing store. ​ ​ -{Golfing Store Narrative} Find P(Y = 2 | X = 1)

Gym Visits Let X represent the number of times a student visits a gym in a one month period.Assume that the probability distribution of X is as follows: ​ ​ -{Gym Visits Narrative} Find the mean μ and the standard deviation σ of this distribution.

Classified Department Phone Calls A classified department receives an average of 10 telephone calls each afternoon between 2 and 4 P.M.The calls occur randomly and independently of one another. ​ ​ -{Classified Department Phone Calls Narrative} Find the probability that the department will receive 13 calls between 2 and 4 P.M.on a particular afternoon.

For a random variable X,if V(cX)= 4V(X),where V refers to the variance,then c must be 2.

The mean of a Poisson distribution,where μ is the average number of successes occurring in a specified interval,is μ.

The time required to drive from New York to New Mexico is a discrete random variable.

The expected return of a two-asset portfolio is equal to the product of the weight assigned to the first asset and the expected return of the first asset plus the product of the weight assigned to the second asset and the expected return of the second asset.

If X and Y are ____________________,the variance of their sum is equal to the sum of their variances.

In the Poisson distribution,the ____________________ is equal to the variance.

If X and Y are independent,then the coefficient of correlation equals ____________________.

Returns on Investment An analysis of the stock market produces the following information about the returns of two stocks. 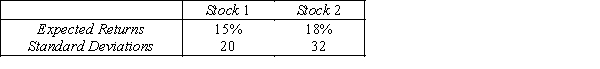Assume that the returns are positively correlated with correlation coefficient of 0.80. ​ ​ -{Returns on Investment Narrative} Suppose that you wish to invest $1 million.Discuss whether you should invest your money in stock 1,stock 2,or a portfolio composed of an equal amount of investments on both stocks.

If the probability of success p remains constant in a binomial distribution,an increase in n will not change the mean.

Shopping Outlet A shopping outlet estimates the probability distribution of the number of stores shoppers actually enter as shown in the table below. ​ ​ -{Shopping Outlet Narrative} Calculate the variance and standard deviation of Y directly from the probability distribution of Y.

The expected number of heads in 100 tosses of an unbiased coin is