Exam 4: Introduction to Probability

Assume you have applied to two different universities (let's refer to them as Universities A and B) for your graduate work. In the past, 25% of students (with similar credentials as yours) who applied to University A were accepted, while University B accepted 35% of the applicants. Assume events are independent of each other. a.What is the probability that you will be accepted in both universities? b.What is the probability that you will be accepted to at least one graduate program? c.What is the probability that one and only one of the universities will accept you? d.What is the probability that neither university will accept you?

If P(A|B) = .3 and P(B) = .8, then

The probability of at least one head in two flips of a coin is

The symbol $\cap$ shows the

Of the last 100 customers entering a computer shop, 25 have purchased a computer. If the classical method for computing probability is used, the probability that the next customer will purchase a computer is

If A and B are independent events with P(A) = 0.4 and P(B) = 0.6, then P(A $\cap$ B) =

A government agency has 6,000 employees. The employees were asked whether they preferred a four-day work week (10 hours per day), a five-day work week (8 hours per day), or flexible hours. You are given information on the employees' responses broken down by gender. 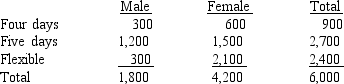a. What is the probability that a randomly selected employee is a man and is in favor of a four-day work week? b. What is the probability that a randomly selected employee is female? c. A randomly selected employee turns out to be female. Compute the probability that she is in favor of flexible hours. d. What percentage of employees is in favor of a five-day work week? e. Given that a person is in favor of flexible time, what is the probability that the person is female? f. What percentage of employees is male and in favor of a five-day work week?

The Ambell Company uses batteries from two different manufacturers. Historically, 60% of the batteries are from manufacturer 1, and 90% of these batteries last for over 40 hours. Only 75% of the batteries from manufacturer 2 last for over 40 hours. A battery in a critical tool fails at 32 hours. What is the probability it was from manufacturer 2?

A committee of 4 is to be selected from a group of 12 people. How many possible committees can be selected?