Question 1

A(n) __________ is a graphical representation in which the sample space is represented by a rectangle and events are represented as circles.

Accepted Answer

A) frequency polygon 
B) histogram 
C) Venn diagram 
D) tree diagram 
A) frequency polygon 
B) histogram 
C) Venn diagram 
D) tree diagram

Question 2

An investment advisor recommends the purchase of shares in Infogenics, Inc. He has made the following predictions:
P(Stock goes up 20% | Rise in GDP) = .6
P(Stock goes up 20% | Level GDP) = .5
P(Stock goes up 20% | Fall in GDP) = .4
An economist has predicted that the probability of a rise in the GDP is 30%, whereas the probability of a fall in the GDP is 40%.
a. Draw a tree diagram to represent this multiple-step experiment.
b. What is the probability that the stock will go up 20%?
c. We have been informed that the stock has gone up 20%. What is the probability of a rise or fall in the GDP?

Accepted Answer

The answer of An investment advisor recommends the purchase of...

Question 3

If P(A) = 0.50, P(B) = 0.60, and P(A $\cap$ B) = 0.30; then events A and B are

Accepted Answer

A) mutually exclusive events 
B) not independent events 
C) independent events 
D) Not enough information is given to answer this question. 
A) mutually exclusive events 
B) not independent events 
C) independent events 
D) Not enough information is given to answer this question.

Question 4

A marina has two party boats available for customers to rent. Historically, demand for party boats has followed this distribution shown below. The revenue per rental is $400. If a customer wants a party boat and none is available, the store gives a $150 coupon for jet ski rental.   
a. What is the expected demand?
b. What is the expected revenue?
c. What is the expected cost?
d. What is the expected profit?

Accepted Answer

a. 1.2
b.

Question 5

A sample point refers to a(n)

Accepted Answer

A) numerical measure of the likelihood of the occurrence of an event 
B) set of all possible experimental outcomes 
C) individual outcome of an experiment 
D) All of these answers are correct. 
A) numerical measure of the likelihood of the occurrence of an event 
B) set of all possible experimental outcomes 
C) individual outcome of an experiment 
D) All of these answers are correct.

Question 6

Tammy is a general contractor and has submitted two bids for two projects (A and B). The probability of getting project A is 0.65. The probability of getting project B is 0.77. The probability of getting at least one of the projects is 0.90.
a.What is the probability that she will get both projects?
b.Are the events of getting the two projects mutually exclusive? Explain, using probabilities.
c.Are the two events independent? Explain, using probabilities.

Accepted Answer

a.0.52
b.No, the pro

Question 7

You are given the following information on Events A, B, C, and D.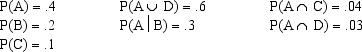   
a. Compute P(D).
b. Compute P(A  B).
c. Compute P(AC).
d. Compute the probability of the complement of C.
e. Are A and B mutually exclusive? Explain your answer.
f. Are A and B independent? Explain your answer.
g. Are A and C mutually exclusive? Explain your answer.
h. Are A and C independent? Explain your answer.

Accepted Answer

a.0.23
b.0.06
c.0.4
d.0.9
e.No

Question 8

Two events, A and B, are mutually exclusive and each has a nonzero probability. If event A is known to occur, the probability of the occurrence of event B is

Accepted Answer

A) one 
B) any positive value 
C) zero 
D) any value between 0 to 1 
A) one 
B) any positive value 
C) zero 
D) any value between 0 to 1

Question 9

Thirty-five percent of the students who enroll in a statistics course go to the statistics laboratory on a regular basis. Past data indicates that 40% of those students who use the lab on a regular basis make a grade of B or better. On the other hand, 10% of students who do not go to the lab on a regular basis make a grade of B or better. If a particular student made an A, determine the probability that she or he used the lab on a regular basis.

Accepted Answer

The answer of Thirty-five percent of the students who enroll...

Question 10

The range of probability is

Accepted Answer

A) any value larger than zero 
B) any value between minus infinity to plus infinity 
C) zero to one 
D) any value between -1 to 1 
A) any value larger than zero 
B) any value between minus infinity to plus infinity 
C) zero to one 
D) any value between -1 to 1

Question 11

If X and Y are mutually exclusive events with P(X) = 0.295, P(Y) = 0.32, then P(X|Y) =

Accepted Answer

A) 0.0944 
B) 0.6150 
C) 1.0000 
D) 0.0000 
A) 0.0944 
B) 0.6150 
C) 1.0000 
D) 0.0000

Question 12

Events that have no sample points in common are

Accepted Answer

A) independent events 
B) posterior events 
C) mutually exclusive events 
D) complements 
A) independent events 
B) posterior events 
C) mutually exclusive events 
D) complements

Question 13

Two of the cylinders in an eight-cylinder car are defective and need to be replaced. If two cylinders are selected at random, what is the probability that
a.both defective cylinders are selected?
b.no defective cylinder is selected?
c.at least one defective cylinder is selected?

Accepted Answer

a.2/56
b.3

Question 14

It is estimated that 3% of the athletes competing in a large tournament are users of an illegal drug to enhance performance. The test for this drug is 90% accurate. What is the probability that an athlete who tests positive is actually a user?

Accepted Answer

The answer of It is estimated that 3% of the...

Question 15

If A and B are independent events with P(A) = 0.4 and P(B) = 0.25, then P(A $\cup$ B) =

Accepted Answer

A) 0.65 
B) 0.55 
C) 0.10 
D) Not enough information is given to answer this question. 
A) 0.65 
B) 0.55 
C) 0.10 
D) Not enough information is given to answer this question.

Question 16

A six-sided die is tossed 3 times. The probability of observing three ones in a row is

Accepted Answer

A) 1/3 
B) 1/6 
C) 1/27 
D) 1/216 
A) 1/3 
B) 1/6 
C) 1/27 
D) 1/216

Question 17

Six vitamin and three sugar tablets identical in appearance are in a box. One tablet is taken at random and given to Person A. A tablet is then selected and given to Person B.What is the probability that
a. Person A was given a vitamin tablet?
b. Person B was given a sugar tablet given that Person A was given a vitamin tablet?
c. neither was given vitamin tablets?
d. both were given vitamin tablets?
e. exactly one person was given a vitamin tablet?
f. Person A was given a sugar tablet and Person B was given a vitamin tablet?
g. Person A was given a vitamin tablet and Person B was given a sugar tablet?

Accepted Answer

a.6/9
b.3/

Question 18

Posterior probabilities are

Accepted Answer

A) simple probabilities 
B) marginal probabilities 
C) joint probabilities 
D) conditional probabilities 
A) simple probabilities 
B) marginal probabilities 
C) joint probabilities 
D) conditional probabilities

Question 19

The complement of P(A | B) is

Accepted Answer

Question 20

A bank has the following data on the gender and marital status of 200 customers.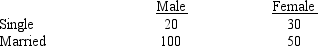   
a. What is the probability of finding a single female customer?
b. What is the probability of finding a married male customer?
c. If a customer is female, what is the probability that she is single?
d. What percentage of customers is male?
e. If a customer is male, what is the probability that he is married?
f. Are gender and marital status mutually exclusive?
g. Is marital status independent of gender? Explain using probabilities.

Accepted Answer

a.0.15
b.0.5
c.0.375
d.60%
e.0

A(n) __________ is a graphical representation in which the sample space is represented by a rectangle and events are represented as circles.

If P(A) = 0.50, P(B) = 0.60, and P(A $\cap$ B) = 0.30; then events A and B are

A sample point refers to a(n)

Two events, A and B, are mutually exclusive and each has a nonzero probability. If event A is known to occur, the probability of the occurrence of event B is

The range of probability is

If X and Y are mutually exclusive events with P(X) = 0.295, P(Y) = 0.32, then P(X|Y) =

Events that have no sample points in common are

Two of the cylinders in an eight-cylinder car are defective and need to be replaced. If two cylinders are selected at random, what is the probability that a.both defective cylinders are selected? b.no defective cylinder is selected? c.at least one defective cylinder is selected?

It is estimated that 3% of the athletes competing in a large tournament are users of an illegal drug to enhance performance. The test for this drug is 90% accurate. What is the probability that an athlete who tests positive is actually a user?

If A and B are independent events with P(A) = 0.4 and P(B) = 0.25, then P(A $\cup$ B) =

A six-sided die is tossed 3 times. The probability of observing three ones in a row is

Posterior probabilities are

The complement of P(A | B) is

Data and Statistics

Descriptive Statistics: Tabular and Graphical Displays

Descriptive Statistics: Numerical Measures

Discrete Probability Distributions

Continuous Probability Distributions

Sampling and Sampling Distributions

Interval Estimation

Hypothesis Tests

Inference About Means and Proportions With Two Populations

Inferences About Population Variances

Tests of Goodness of Fit, Independence and Multiple Proportions

Experimental Design and Analysis of Variance

Simple Linear Regression

Multiple Regression

Regression Analysis: Model Building

Time Series Analysis and Forecasting

Nonparametric Methods

Statistical Methods for Quality Control

Decision Analysis

Sample Survey

Filters

Exam 4: Introduction to Probability

A(n) __________ is a graphical representation in which the sample space is represented by a rectangle and events are represented as circles.

If P(A) = 0.50, P(B) = 0.60, and P(A ∩\cap∩ B) = 0.30; then events A and B are

A sample point refers to a(n)

Two events, A and B, are mutually exclusive and each has a nonzero probability. If event A is known to occur, the probability of the occurrence of event B is

The range of probability is

If X and Y are mutually exclusive events with P(X) = 0.295, P(Y) = 0.32, then P(X|Y) =

Events that have no sample points in common are

Two of the cylinders in an eight-cylinder car are defective and need to be replaced. If two cylinders are selected at random, what is the probability that a.both defective cylinders are selected? b.no defective cylinder is selected? c.at least one defective cylinder is selected?

It is estimated that 3% of the athletes competing in a large tournament are users of an illegal drug to enhance performance. The test for this drug is 90% accurate. What is the probability that an athlete who tests positive is actually a user?

If A and B are independent events with P(A) = 0.4 and P(B) = 0.25, then P(A ∪\cup∪ B) =

A six-sided die is tossed 3 times. The probability of observing three ones in a row is

Posterior probabilities are

The complement of P(A | B) is

Data and Statistics

Descriptive Statistics: Tabular and Graphical Displays

Descriptive Statistics: Numerical Measures

Discrete Probability Distributions

Continuous Probability Distributions

Sampling and Sampling Distributions

Interval Estimation

Hypothesis Tests

Inference About Means and Proportions With Two Populations

Inferences About Population Variances

Tests of Goodness of Fit, Independence and Multiple Proportions

Experimental Design and Analysis of Variance

Simple Linear Regression

Multiple Regression

Regression Analysis: Model Building

Time Series Analysis and Forecasting

Nonparametric Methods

Statistical Methods for Quality Control

Decision Analysis

Sample Survey

Filters

If P(A) = 0.50, P(B) = 0.60, and P(A $\cap$ B) = 0.30; then events A and B are

If A and B are independent events with P(A) = 0.4 and P(B) = 0.25, then P(A $\cup$ B) =