Exam 5: Discrete Probability Distributions

Consider a Poisson probability distribution in a process with an average of 3 flaws every 100 feet. Find the probability of a. no flaws in 100 feet b. 2 flaws in 100 feet c. 1 flaws in 150 feet d. 3 or 4 flaws in 150 feet

Four percent of the customers of a mortgage company default on their payments. A sample of five customers is selected. What is the probability that exactly two customers in the sample will default on their payments?

When a particular machine is functioning properly, 80% of the items produced are non-defective. If three items are examined, what is the probability that one is defective? Use the binomial probability function to answer this question.

The standard deviation of a binomial distribution is

A random variable x has the following probability distribution: a.Determine the expected value of x. b.Determine the variance.

Excel's __________ function can be used to compute the variance of a discrete random variable.

An experiment consists of making 80 telephone calls in order to sell a particular insurance policy. The random variable in this experiment is the number of sales made. This random variable is a

In a binomial experiment consisting of five trials, the number of different values that x (the number of successes) can assume is

Exhibit 5-1 The following represents the probability distribution for the daily demand of microcomputers at a local store. -Refer to Exhibit 5-1. The probability of having a demand for at least two microcomputers is

Exhibit 5-8 The student body of a large university consists of 60% female students. A random sample of 8 students is selected. -Refer to Exhibit 5-8. What is the probability that among the students in the sample exactly two are female?

Excel's BINOM.DIST function has how many inputs?

Exhibit 5-3 The probability distribution for the number of goals the Lions soccer team makes per game is given below. -Refer to Exhibit 5-3. The expected number of goals per game is

Exhibit 5-9 Forty percent of all registered voters in a national election are female. A random sample of 5 voters is selected. -Refer to Exhibit 5-9. What is the random variable in this experiment?

A measure of the average value of a random variable is called a(n)

The weight of an object, measured in grams, is an example of

The expected value of a random variable is the

A continuous random variable may assume

In a large corporation, 65% of the employees are male. A random sample of five employees is selected. a.Define the random variable in words for this experiment. b.What is the probability that the sample contains exactly three male employees? c.What is the probability that the sample contains no male employees? d.What is the probability that the sample contains more than three female employees? e.What is the expected number of female employees in the sample?

Exhibit 5-5 AMR is a computer-consulting firm. The number of new clients that they have obtained each month has ranged from 0 to 6. The number of new clients has the probability distribution that is shown below. 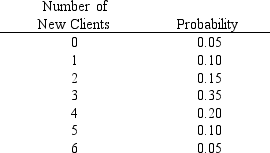-Refer to Exhibit 5-5. The expected number of new clients per month is

Telephone calls arrive at the Global Airline reservation office in Louisville according to a Poisson distribution with a mean of 1.2 calls per minute. a. What is the probability of receiving exactly one call during a one-minute interval? b. What is the probability of receiving at most 2 calls during a one-minute interval? c. What is the probability of receiving at least two calls during a one-minute interval? d. What is the probability of receiving exactly 4 calls during a five-minute interval? e. What is the probability that at most 2 minutes elapse between one call and the next?