Exam 5: Discrete Probability Distributions

A salesperson contacts eight potential customers per day. From past experience, we know that the probability of a potential customer making a purchase is 0.10. a.Define the random variable in words for this experiment. b.What is the probability the salesperson will make exactly two sales in a day? c.What is the probability the salesperson will make at least two sales in a day? d.What percentage of days will the salesperson not make a sale? e.What is the expected number of sales per day?

The variance is a weighted average of the

An example of a bivariate experiment is

The expected value for a binomial probability distribution is

Which of the following is not a required condition for a discrete probability function?

The number of customers at Winkies Donuts between 8:00a.m. and 9:00a.m. is believed to follow a Poisson distribution with a mean of 2 customers per minute. a. During a randomly selected one-minute interval during this time period, what is the probability of 6 customers arriving to Winkies? b. What is the probability that at least 2 minutes elapse between customer arrivals?

In a southern state, it was revealed that 5% of all automobiles in the state did not pass inspection. Of the next ten automobiles entering the inspection station, a. what is the probability that none will pass inspection? b. what is the probability that all will pass inspection? c. what is the probability that exactly two will not pass inspection? d. what is the probability that more than three will not pass inspection? e. what is the probability that fewer than two will not pass inspection? f. Find the expected number of automobiles not passing inspection. g. Determine the standard deviation for the number of cars not passing inspection.

Exhibit 5-10 The probability that Pete will catch fish on a particular day when he goes fishing is 0.8. Pete is going fishing 3 days next week. -Excel's POISSON.DIST function can be used to compute

Exhibit 5-5 AMR is a computer-consulting firm. The number of new clients that they have obtained each month has ranged from 0 to 6. The number of new clients has the probability distribution that is shown below. 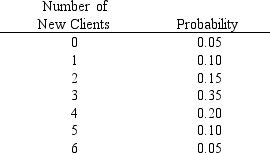-The number of electrical outages in a city varies from day to day. Assume that the number of electrical outages (x) in the city has the following probability distribution. The mean and the standard deviation for the number of electrical outages (respectively) are

Exhibit 5-7 A sample of 2,500 people was asked how many cups of coffee they drink in the morning. You are given the following sample information. -Which of the following is not a characteristic of an experiment where the binomial probability distribution is applicable?

A retailer of electronic equipment received six Blu-ray players from the manufacturer. Three of the players were damaged in the shipment. The retailer sold two players to two customers.a Can a binomial formula be used for the solution of the above problem? b.What kind of probability distribution does the above satisfy, and is there a function for solving such problems? c.What is the probability that both customers received damaged players? d.What is the probability that one of the two customers received a defective player?

Exhibit 5-8 The student body of a large university consists of 60% female students. A random sample of 8 students is selected. -Refer to Exhibit 5-8. What is the probability that among the students in the sample at least 7 are female?

A life insurance company has determined that each week an average of seven claims is filed in its Nashville branch. a.Define the random variable in words for this experiment. b.What is the probability that during the next week exactly seven claims will be filed? c.What is the probability that during the next week no claims will be filed? d.What is the probability that during the next week fewer than four claims will be filed? e.What is the probability that during the next week at least seventeen claims will be filed?

Which of the following is(are) required condition(s) for a discrete probability function?

For the following probability distribution: 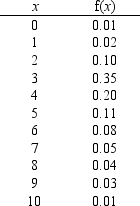a.Determine E(x). b.Determine the variance and the standard deviation.

The records of a department store show that 20% of its customers who make a purchase return the merchandise in order to exchange it. In the next six purchases, a.what is the probability that three customers will return the merchandise for exchange? b.what is the probability that four customers will return the merchandise for exchange? c.what is the probability that none of the customers will return the merchandise for exchange?

Twenty-five percent of the employees of a large company are minorities. A random sample of 7 employees is selected. a. Define the random variable in words for this experiment. b. What is the probability that the sample contains exactly 4 minorities? c. What is the probability that the sample contains fewer than 2 minorities? d. What is the probability that the sample contains exactly 1 non-minority? e. What is the expected number of minorities in the sample? f. What is the variance of the minorities?

The weight of an object, measured to the nearest gram, is an example of

Exhibit 5-10 The probability that Pete will catch fish on a particular day when he goes fishing is 0.8. Pete is going fishing 3 days next week. -The Poisson probability distribution is used with

Only 0.02% of credit card holders of a company report the loss or theft of their credit cards each month. The company has 15,000 credit cards in the city of Memphis. What is the probability that during the next month in the city of Memphis a. no one reports the loss or theft of their credit cards? b. every credit card is lost or stolen? c. six people report the loss or theft of their cards? d. at least nine people report the loss or theft of their cards? e. Determine the expected number of reported lost or stolen credit cards. f. Determine the standard deviation for the number of reported lost or stolen cards.