Exam 9: Hypothesis Tests
Exam 1: Data and Statistics85 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays112 Questions
Exam 3: Descriptive Statistics: Numerical Measures139 Questions
Exam 4: Introduction to Probability129 Questions
Exam 5: Discrete Probability Distributions150 Questions
Exam 6: Continuous Probability Distributions144 Questions
Exam 7: Sampling and Sampling Distributions119 Questions
Exam 8: Interval Estimation118 Questions
Exam 9: Hypothesis Tests118 Questions
Exam 10: Inference About Means and Proportions With Two Populations127 Questions
Exam 11: Inferences About Population Variances113 Questions
Exam 12: Tests of Goodness of Fit, Independence and Multiple Proportions76 Questions
Exam 13: Experimental Design and Analysis of Variance125 Questions
Exam 14: Simple Linear Regression103 Questions
Exam 15: Multiple Regression109 Questions
Exam 16: Regression Analysis: Model Building82 Questions
Exam 17: Time Series Analysis and Forecasting80 Questions
Exam 18: Nonparametric Methods83 Questions
Exam 19: Statistical Methods for Quality Control75 Questions
Exam 20: Decision Analysis71 Questions
Exam 21: Sample Survey68 Questions
Select questions type
Which Excel function would not be appropriate to use when conducting a hypothesis test for a population proportion?
(Multiple Choice)
4.8/5  (37)
(37)
Read the z statistic from the normal distribution table and circle the correct answer. A one-tailed test (lower tail) at a .063 level of significance; z =
(Multiple Choice)
4.9/5  (37)
(37)
You are given the following information obtained from a random sample of 5 observations. 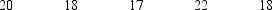 At a 10% level of significance, use Excel to determine whether or not the mean of the population from which this sample was taken is significantly less than 21. (Assume the population is normally distributed.)
At a 10% level of significance, use Excel to determine whether or not the mean of the population from which this sample was taken is significantly less than 21. (Assume the population is normally distributed.)
(Essay)
4.9/5  (41)
(41)
A meteorologist stated that the average temperature during July in Chattanooga was 80 degrees. A sample of 32 Julys was taken. The correct set of hypotheses is
(Multiple Choice)
4.7/5  (31)
(31)
Read the z statistic from the normal distribution table and circle the correct answer. A one-tailed test (upper tail) at a .123 level of significance; z =
(Multiple Choice)
4.9/5  (27)
(27)
Exhibit 9-1  -Refer to Exhibit 9-1. If the test is done at a .05 level of significance, the null hypothesis should
-Refer to Exhibit 9-1. If the test is done at a .05 level of significance, the null hypothesis should
(Multiple Choice)
4.7/5  (39)
(39)
The academic planner of a university thinks that at least 35% of the entire student body attends summer school. The correct set of hypotheses to test his belief is
(Multiple Choice)
5.0/5  (35)
(35)
A manufacturer claims that at least 40% of its customers use coupons. A study of 25 customers is undertaken to test that claim. The results of the study follow. 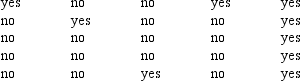 At a .05 level of significance, use Excel to test the manufacturer's claim.
At a .05 level of significance, use Excel to test the manufacturer's claim.
(Essay)
4.8/5  (42)
(42)
For a two-tailed hypothesis test about , we can use any of the following approaches except
(Multiple Choice)
4.8/5  (35)
(35)
Exhibit 9-3  -Refer to Exhibit 9-3. If the test is done at a 5% level of significance, the null hypothesis should
-Refer to Exhibit 9-3. If the test is done at a 5% level of significance, the null hypothesis should
(Multiple Choice)
4.7/5  (35)
(35)
Exhibit 9-6
A random sample of 100 people was taken. Eighty of the people in the sample favored Candidate A. We are interested in determining whether or not the proportion of the population in favor of Candidate A is significantly more than 75%.
-The rejection region for a one-tailed hypothesis test
(Multiple Choice)
4.9/5  (48)
(48)
The board of directors of a corporation has agreed to allow the human resources manager to move to the next step in planning day care service for employees' children if the manager can prove that at least 25% of the employees have interest in using the service. The HR manager polls 300 employees and 90 say they would seriously consider utilizing the service. At the = .10 level of significance, is there enough interest in the service to move to the next planning step?
(Essay)
4.9/5  (44)
(44)
Excel's __________ function can be used to calculate a p-value for a hypothesis test.
(Multiple Choice)
4.8/5  (42)
(42)
When using Excel to calculate a p-value for a lower-tail hypothesis test, the following must be used
(Multiple Choice)
4.9/5  (40)
(40)
The sponsors of televisions shows targeted at the market of 5 - 8 year olds want to test the hypothesis that children watch television at most 20 hours per week. The population of viewing hours per week is known to be normally distributed with a standard deviation of 6 hours. A market research firm conducted a random sample of 30 children in this age group. The resulting data follows:  At a .10 level of significance, use Excel to test the sponsors' hypothesis.
At a .10 level of significance, use Excel to test the sponsors' hypothesis.
(Essay)
4.8/5  (36)
(36)
Exhibit 9-6
A random sample of 100 people was taken. Eighty of the people in the sample favored Candidate A. We are interested in determining whether or not the proportion of the population in favor of Candidate A is significantly more than 75%.
-If a hypothesis test has a Type I error probability of .05, that means
(Multiple Choice)
4.8/5  (35)
(35)
A student believes that the average grade on the statistics final examination is 87. A sample of 36 final examinations is taken. The average grade in the sample is 83.96. The population variance is 144.
a.State the null and alternative hypotheses.
b.Using a critical value, test the hypothesis at the 5% level of significance.
c.Using a p-value, test the hypothesis at the 5% level of significance.
d.Using a confidence interval, test the hypothesis at the 5% level of significance.
e.Compute the probability of a Type II error if the average grade on the final is 85.
(Essay)
4.9/5  (34)
(34)
At a certain manufacturing plant, a machine produces ball bearings that should have a diameter of 0.500 mm. If the machine produces ball bearings that are either too small or too large, the ball bearings must be scrapped. Every hour, a quality control manager takes a random sample of 36 ball bearings to test to see if the process is "out of control" (i.e. to test to see if the average diameter differs from 0.500 mm). Assume that the process is maintaining the desired standard deviation of .06 mm. The results from the latest sample follow:  At a .01 level of significance, use Excel to test whether the process is "out of control."
At a .01 level of significance, use Excel to test whether the process is "out of control."
(Essay)
4.9/5  (37)
(37)
Showing 61 - 80 of 118
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)