Exam 9: Hypothesis Tests

Exhibit 9-6 A random sample of 100 people was taken. Eighty of the people in the sample favored Candidate A. We are interested in determining whether or not the proportion of the population in favor of Candidate A is significantly more than 75%. -"D" size batteries produced by MNM Corporation have had a life expectancy of 87 hours. Because of an improved production process, the company believes that there has been an increase in the life expectancy of its "D" size batteries. A sample of 36 batteries showed an average life of 88.5 hours. Assume from past information that it is known that the standard deviation of the population is 9 hours. a.Use a 0.01 level of significance, and test to determine if there has been an increase in the life expectancy of the "D" size batteries. b.What is the p-value associated with the sample results? What is your conclusion, based on the p-value?

Exhibit 9-6 A random sample of 100 people was taken. Eighty of the people in the sample favored Candidate A. We are interested in determining whether or not the proportion of the population in favor of Candidate A is significantly more than 75%. -A lathe is set to cut bars of steel into lengths of 6 centimeters. The lathe is considered to be in perfect adjustment if the average length of the bars it cuts is 6 centimeters. A sample of 121 bars is selected randomly and measured. It is determined that the average length of the bars in the sample is 6.08 centimeters. The population standard deviation is 0.44 centimeters. Determine whether or not the lathe is in perfect adjustment. Use a .05 level of significance.

A group of young businesswomen wish to open a high fashion boutique in a vacant store, but only if the average income of households in the area is more than $45,000. A random sample of 9 households showed the following results. 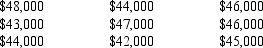Use the statistical techniques in Excel to advise the group on whether or not they should locate the boutique in this store. Use a .05 level of significance. (Assume the population is normally distributed.)

If a hypothesis is not rejected at a 5% level of significance, it will

Exhibit 9-6 A random sample of 100 people was taken. Eighty of the people in the sample favored Candidate A. We are interested in determining whether or not the proportion of the population in favor of Candidate A is significantly more than 75%. -In a two-tailed hypothesis test, the null hypothesis should be rejected if the p-value is

When the p-value is used for hypothesis testing, the null hypothesis is rejected if

A student believes that no more than 20% (i.e., $\le$ 20%) of the students who finish a statistics course get an A. A random sample of 100 students was taken. Twenty-four percent of the students in the sample received A's. a.State the null and alternative hypotheses. b.Using a critical value, test the hypothesis at the 1% level of significance. c.Using a p-value, test the hypothesis at the 1% level of significance.

In the past the average age of employees of a large corporation has been 40 years. Recently, the company has been hiring older individuals. In order to determine whether there has been an increase in the average age of all the employees, a sample of 25 employees was selected. The average age in the sample was 45 years with a standard deviation of 5 years. Assume the distribution of the population is normal. Let $\alpha$ = .05. a.State the null and the alternative hypotheses. b.Test to determine whether or not the mean age of all employees is significantly more than 40 years.

Consider the following hypothesis test: H_o: p = 0.5 H_a: p $\neq$ 0.5 A sample of 800 provided a sample proportion of 0.58. a.Using $\alpha$ = 0.05, what is the rejection rule? b.Determine the standard error of the proportion. c.Compute the value of the test statistic z. What is your conclusion? d.Determine the p-value.

A Type I error is committed when

Exhibit 9-2 The manager of a grocery store has taken a random sample of 100 customers. The average length of time it took the customers in the sample to check out was 3.1 minutes. The population standard deviation is known to be 0.5 minutes. We want to test to determine whether or not the mean waiting time of all customers is significantly more than 3 minutes. -Refer to Exhibit 9-2. At a .05 level of significance, it can be concluded that the mean of the population is

The probability of making a Type I error is denoted by

A Type II error is committed when

The school's newspaper reported that the proportion of students majoring in business is at least 30%. You plan on taking a sample to test the newspaper's claim. The correct set of hypotheses is

Exhibit 9-6 A random sample of 100 people was taken. Eighty of the people in the sample favored Candidate A. We are interested in determining whether or not the proportion of the population in favor of Candidate A is significantly more than 75%. -For a two-tailed hypothesis test about a population mean, the null hypothesis can be rejected if the confidence interval

Exhibit 9-4 A random sample of 16 students selected from the student body of a large university had an average age of 25 years. We want to determine if the average age of all the students at the university is significantly different from 24. Assume the distribution of the population of ages is normal with a standard deviation of 2 years. -Refer to Exhibit 9-4. At a .05 level of significance, it can be concluded that the mean age is

The average life expectancy of tires produced by the Whitney Tire Company has been 40,000 miles. Management believes that due to a new production process, the life expectancy of its tires has increased. In order to test the validity of this belief, the correct set of hypotheses is

Exhibit 9-6 A random sample of 100 people was taken. Eighty of the people in the sample favored Candidate A. We are interested in determining whether or not the proportion of the population in favor of Candidate A is significantly more than 75%. -A researcher is testing a new painkiller that claims to relieve pain in less than 15 minutes, on average. a.State the hypotheses associated with the researcher's test. b.Describe a Type I error for this situation. c.Describe a Type II error for this situation.