Exam 18: Project Management
A company wants to develop a project using PERT to modify one of their products which has poor sales. They have determined the following activities, precedence relationships and time estimates in days for the project:
Immediate Optiristic Most Likely Pessimistic Activity Predecessors a mone 4 6 7 b a 1 2 3 c a 5 5 5 d b 7 9 12 E b 2 4 8 f c, d 6 9 10
a. What is the expected duration for activity a?
b. What is the variance for activity d?
c. How many paths are there in the network?
d. What is the earliest start ES) time for activity e?
e. What is the slack in days for activity b?f. What is the critical path
g. What is the duration of the critical path in days
h. What is the standard deviation of the critical path
i. What is the probability that the project will take longer than 28 weeks to complete?
To answer these questions, we will use the Program Evaluation and Review Technique (PERT) calculations. PERT is a project management tool used to schedule, organize, and coordinate tasks within a project.a. Expected duration for activity a:
The expected duration (TE) for an activity in PERT is calculated using the formula:
For activity a:
b. Variance for activity d:
The variance of an activity in PERT is calculated using the formula:
For activity d:
c. Number of paths in the network:
To determine the number of paths, we need to trace the paths from the start to the end of the project. The paths are:
1. a -> b -> d -> f
2. a -> c -> f
3. a -> b -> e (Note: This is not a complete path to the end of the project, so it is not counted)
So, there are 2 paths in the network.
d. Earliest start (ES) time for activity e:
The earliest start time for an activity is the earliest finish time of its immediate predecessor(s). Activity e can only start after activity b is finished.
To find EF_b, we need to calculate the expected duration for activity b:
Since activity a is the predecessor of b and its expected duration is 5.83 days, the earliest finish for b is:
Therefore, the earliest start for e is 7.83 days.
e. Slack in days for activity b:
Slack or float is the amount of time that an activity can be delayed without delaying the project. Since activity b is on the critical path (as we will see in part f), its slack is 0 days.
f. Critical path:
The critical path is the longest path through the network, which determines the shortest time to complete the project. To find the critical path, we calculate the expected duration for all activities and paths:
Path 1: a -> b -> d -> f
Path 2: a -> c -> f
The critical path is Path 1 (a -> b -> d -> f) since it has the longest duration.
g. Duration of the critical path in days:
From part f, the duration of the critical path (Path 1) is 25.83 days.
h. Standard deviation of the critical path:
The standard deviation of the critical path is the square root of the sum of the variances of the activities on the critical path. We only calculated the variance for activity d, but we would need the variances for activities a, b, and f as well to calculate the standard deviation of the critical path. Assuming we have those variances, the standard deviation would be:
Without the variances for a, b, and f, we cannot calculate the standard deviation.
i. Probability that the project will take longer than 28 weeks to complete:
To calculate this probability, we would need the standard deviation of the critical path, which we do not have. Additionally, 28 weeks is equivalent to 196 days, which is significantly longer than the duration of the critical path calculated in part g. Therefore, without further information, we can assume the probability of the project taking longer than 28 weeks is extremely low or effectively zero, given the current estimates.
Which of the following is not considered a project?
C
Define a project. Give some non-manufacturing or non-construction examples.
A project is a temporary and often customized initiative that consists of many smaller tasks and activities that must be coordinated and completed to finish the entire initiative on time and within budget. Students, for example, should identify projects relevant to them such as conducting a term assignment or setting up a banquet for a student organization.
List at least (six principal factors contributors) to project success.
A statement of work would be developed in the "Organize" step of the project life cycle.
A slack of -2) means the project is ahead of schedule by two time periods.
The following network shows all the major activities on the circles nodes). Each node contains time estimates in weeks. 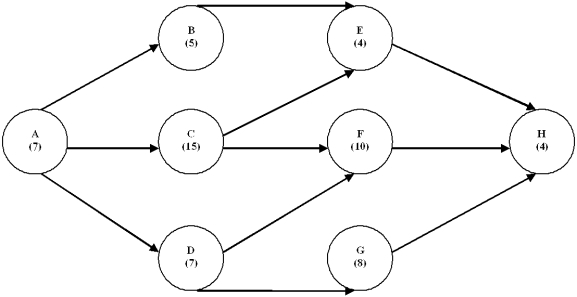 Complete the following table.
Activity Time Earliest Start Earliest Finish Latest Start Latest Finish Slack On Critical Path? B C G
Complete the following table.
Activity Time Earliest Start Earliest Finish Latest Start Latest Finish Slack On Critical Path? B C G
In which stage in the project life cycle would crashing likely be performed?
Explain the role of the project managers and some principles for success.
Strong leadership is an impediment to project management success because of the team-based nature of most projects.
A manufacturing company is planning to use PERT to setup a project for a new production line. For this project, they have established the following activities, precedence relationships, and time estimates in days:
Activity Immediate Predecessors a none 8 10 12 b none 6 7 9 c b 3 3 3 d a 10 15 20 E d 6 7 8 f c 9 10 11 E d 5 7 10 h ef 14 15 16
a. What is the expected duration for activity b?
b. What is the variance of activity d?
c. How many paths are there in the network?
d. What is the earliest finish EF) time for activity e?
e. What is the slack in days for activity c
f. What is the critical path
g. What is the duration of the critical path in days
h. What is the standard deviation of the critical path
i. What is the probability of completing the project within 50 days?
Which step in the project management process would involve developing alternative plans in anticipation of problems that might arise?
Which of the following is least related to Program Evaluation and Review Technique (PERT)?
A type of organization that can result in inefficiencies because of duplication of resources across the organization is called
Activity times must be estimated from historical data of similar work tasks to provide realism for a project.
The critical path is the sequence of activities that takes the longest time.
Which of the following is incorrect regarding time/cost trade-offs?
Using a beta probability distribution to characterize uncertain activity times is practical because it allows managers to use judgmental estimates to identify the distribution.
Define critical path and explain how it is identified once a project schedule is calculated
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)