After determining whether the variation model below is of the form $y = k x$ or $y = \frac { k } { x }$ ,find the value of k. \[\begin{array} { | c | c | c | c | c | c | } \hline x & 20 & 40 & 60 & 80 & 100 \\ \hline y & \frac { 1 } { 30 } & \frac { 1 } { 60 } & \frac { 1 } { 90 } & \frac { 1 } { 120 } & \frac { 1 } { 150 } \\ \hline \end{array}\]

A) $k = \frac { 1 } { 20 }$ B) $k = \frac { 3 } { 2 }$ C) $k = \frac { 5 } { 4 }$ D) $k = \frac { 1 } { 10 }$ E) $k = \frac { 2 } { 3 }$ A) $k = \frac { 1 } { 20 }$ B) $k = \frac { 3 } { 2 }$ C) $k = \frac { 5 } { 4 }$ D) $k = \frac { 1 } { 10 }$ E) $k = \frac { 2 } { 3 }$

Use the given value of k to complete the table for the direct variation model $y = k x ^ { 2 }$ . Plot the points on a rectangular coordinate system. \[\begin{array}{l} \begin{array} { | l | l | l | l | l | l | } \hline x & 8 & 10 & 12 & 14 & 16 \\ \hline y = k x ^ { 2 } & & & & & \\ & & & & & \\ \hline \end{array}\\ k = 1 \end{array}\]

A) \[\begin{array} { | c | c | c | c | c | c | } \hline x & 8 & 10 & 12 & 14 & 16 \\ \hline y = k x ^ { 2 } & 256 & 196 & 144 & 100 & 64 \\ \hline \end{array}\] B) \[\begin{array} { | c | c | c | c | c | c | } \hline x & 8 & 10 & 12 & 14 & 16 \\ \hline y = k x ^ { 2 } & 64 & 100 & 144 & 196 & 256 \\ \hline \end{array}\] C) \[\begin{array} { | c | c | c | c | c | c | } \hline x & 8 & 10 & 12 & 14 & 16 \\ \hline y = k x ^ { 2 } & 64 & 64 & 64 & 64 & 64 \\ \hline \end{array}\] D) \[\begin{array} { | c | c | c | c | c | c | } \hline x & 8 & 10 & 12 & 14 & 16 \\ \hline y = k x ^ { 2 } & 64 & 100 & 144 & 100 & 64 \\ \hline \end{array}\] E) \[\begin{array} { | c | c | c | c | c | c | } \hline x & 8 & 10 & 12 & 14 & 16 \\ \hline y = k x ^ { 2 } & 8 & 10 & 12 & 14 & 16 \\ & & & & & \\ \hline \end{array}\] A) \[\begin{array} { | c | c | c | c | c | c | } \hline x & 8 & 10 & 12 & 14 & 16 \\ \hline y = k x ^ { 2 } & 256 & 196 & 144 & 100 & 64 \\ \hline \end{array}\] B) \[\begin{array} { | c | c | c | c | c | c | } \hline x & 8 & 10 & 12 & 14 & 16 \\ \hline y = k x ^ { 2 } & 64 & 100 & 144 & 196 & 256 \\ \hline \end{array}\] C) \[\begin{array} { | c | c | c | c | c | c | } \hline x & 8 & 10 & 12 & 14 & 16 \\ \hline y = k x ^ { 2 } & 64 & 64 & 64 & 64 & 64 \\ \hline \end{array}\] D) \[\begin{array} { | c | c | c | c | c | c | } \hline x & 8 & 10 & 12 & 14 & 16 \\ \hline y = k x ^ { 2 } & 64 & 100 & 144 & 100 & 64 \\ \hline \end{array}\] E) \[\begin{array} { | c | c | c | c | c | c | } \hline x & 8 & 10 & 12 & 14 & 16 \\ \hline y = k x ^ { 2 } & 8 & 10 & 12 & 14 & 16 \\ & & & & & \\ \hline \end{array}\]

Determine whether the variation model is of the form $y = k x$ or $y = \frac { k } { x }$ and find k.Then write a model that relates y and x. \[\begin{array} { | c | c | c | c | c | c | } \hline x & 4 & 8 & 12 & 16 & 20 \\ \hline y & 1 & \frac { 1 } { 2 } & \frac { 1 } { 3 } & \frac { 1 } { 4 } & \frac { 1 } { 5 } \\ \hline \end{array}\]

A) $y = 4 x$ B) $y = \frac { 1 } { x }$ C) $y = \frac { 4 } { x }$ D) $y = x$ E) $y = \frac { x } { 4 }$ A) $y = 4 x$ B) $y = \frac { 1 } { x }$ C) $y = \frac { 4 } { x }$ D) $y = x$ E) $y = \frac { x } { 4 }$

After determining whether the variation model below is of the form $y = k x$ or $y = \frac { k } { x }$ ,find the value of k. \[\begin{array} { | c | c | c | c | c | c | } \hline x & 154 & 161 & 168 & 175 & 182 \\ \hline y & 66 & 69 & 72 & 75 & 78 \\ \hline \end{array}\]

A) $k = 7$ B) $k = \frac { 7 } { 3 }$ C) $k = \frac { 1 } { 7 }$ D) $k = \frac { 3 } { 7 }$ E) $k = \frac { 7 } { 66 }$ A) $k = 7$ B) $k = \frac { 7 } { 3 }$ C) $k = \frac { 1 } { 7 }$ D) $k = \frac { 3 } { 7 }$ E) $k = \frac { 7 } { 66 }$

Determine whether the variation model is of the form $y = k x$ or $y = \frac { k } { x }$ and find k.Then write a model that relates y and x. \[\begin{array} { | c | c | c | c | c | c | } \hline x & 5 & 10 & 15 & 20 & 25 \\ \hline y & 26 & 13 & \frac { 26 } { 3 } & \frac { 13 } { 2 } & \frac { 26 } { 5 } \\ \hline \end{array}\]

A) $y = \frac { 130 } { x }$ B) $y = \frac { x } { 130 }$ C) $y = \frac { 1 } { x }$ D) $y = 130 x$ E) $y = x$ A) $y = \frac { 130 } { x }$ B) $y = \frac { x } { 130 }$ C) $y = \frac { 1 } { x }$ D) $y = 130 x$ E) $y = x$

Exam 10: Mathematical Modeling and Variation

Find a mathematical model representing the statement.(Determine the constant of proportionality. ) Z varies jointly as x and y. $( z = 128 \text { when } x = 4 \text { and } y = 8 . )$

(Multiple Choice)

4.9/5

(35)

Question 21

The simple interest on an investment is directly proportional to the amount of the investment.By investing $5800 in a municipal bond,you obtained an interest payment of $221.25 after 1 year.Find a mathematical model that gives the interest I for this municipal bond after 1 year in terms of the amount invested P.(Round your answer to three decimal places. )

(Multiple Choice)

4.8/5

(45)

Question 22

The simple interest on an investment is directly proportional to the amount of the investment.By investing $2400 in a certain bond issue,you obtained an interest payment of $111.75 after 1 year.Find a mathematical model that gives the interest I for this bond issue after 1 year in terms of the amount invested P.(Round your answer to three decimal places. )

(Multiple Choice)

4.8/5

(36)

Question 23

The work W (in joules)done when lifting an object varies jointly with the mass m (in kilograms)of the object and the height h (in meters)that the object is lifted.The work done when a 120-kilogram object is lifted 1.8 meters is 2116.8 joules.How much work is done when lifting a 200-kilogram object 1.5 meters?

(Multiple Choice)

4.9/5

(30)

Question 24

After determining whether the variation model below is of the form $y = k x$ or $y = \frac { k } { x }$ ,find the value of k. x 20 40 60 80 100 y

(Multiple Choice)

4.9/5

(32)

Question 25

Use the given value of k to complete the table for the direct variation model $y = k x ^ { 2 }$ . Plot the points on a rectangular coordinate system. x 8 10 12 14 16 y=k k=1

(Multiple Choice)

4.9/5

(28)

Question 26

Find a mathematical model representing the statement.(Determine the constant of proportionality. ) Z varies directly as the square of x and inversely as y.(z = 36 when x = 9 and y = 3. )

(Multiple Choice)

4.8/5

(32)

Question 27

Determine whether the variation model is of the form $y = k x$ or $y = \frac { k } { x }$ and find k.Then write a model that relates y and x. x 4 8 12 16 20 y 1

(Multiple Choice)

4.7/5

(30)

Question 28

The simple interest on an investment is directly proportional to the amount of the investment.By investing $6000 in a certain certificate of deposit,you obtained an interest payment of $276.00 after 1 year.Determine a mathematical model that gives the interest,I ,for this CD after 1 year in terms of the amount invested,P.

(Multiple Choice)

4.8/5

(37)

Question 29

Use the given value of k to complete the table for the inverse variation model $y = \frac { k } { x ^ { 2 } }$ Plot the points on a rectangular coordinate system. x 2 4 6 8 10 y= k=2

(Multiple Choice)

5.0/5

(38)

Question 30

A force of $f = 225$ newtons stretches a spring $s = 0.15$ meter (see figure). 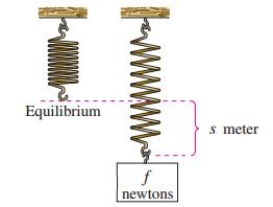How far will a force of 60 newtons stretch the spring? What force is required to stretch the spring 0.1 meter?

(Multiple Choice)

4.8/5

(34)

Question 31

Assume that y is directly proportional to x.Use the given x-value and y-value to find a linear model that relates y and x. $x = 5 , y = 24$

(Multiple Choice)

4.8/5

(34)

Question 32

After determining whether the variation model below is of the form $y = k x$ or $y = \frac { k } { x }$ ,find the value of k. x 154 161 168 175 182 y 66 69 72 75 78

(Multiple Choice)

4.8/5

(42)

Question 33

Assume that y is directly proportional to x.If x = 28 and y = 21,determine a linear model that relates y and x.

(Multiple Choice)

4.8/5

(31)

Question 34

Use the fact that the resistance of a wire carrying an electrical current is directly proportional to its length and inversely proportional to its cross-sectional area. A 10-foot piece of copper wire produces a resistance of 0.2 ohm.Use the constant of proportionality k = 0.000833 to find the diameter of the wire. (Round the answer up to three decimal places. )

(Multiple Choice)

4.8/5

(38)

Question 35

Determine whether the variation model is of the form $y = k x$ or $y = \frac { k } { x }$ and find k.Then write a model that relates y and x. x 9 18 27 36 45 y 2 4 6 8 10

(Multiple Choice)

4.9/5

(34)

Question 36

Find a mathematical model representing the statement.(Determine the constant of proportionality. ) Y is inversely proportional to x. $( y = 7 \text { when } x = 5 . )$

(Multiple Choice)

4.9/5

(39)

Question 37

Property tax is based on the assessed value of a property.A house that has an assessed value of $200,000 has a property tax of $4,820.Find a mathematical model that gives the amount of property tax y in terms of the assessed value x of the property.Use the model to find the property tax on a house that has an assessed value of $230,000.(Round your answer to four decimal places. )

(Multiple Choice)

4.8/5

(39)

Question 38

A force of 270 newtons stretches a spring 0.18 meter.What force is required to stretch the spring 0.19 meter?

(Multiple Choice)

4.8/5

(45)

Question 39

Determine whether the variation model is of the form $y = k x$ or $y = \frac { k } { x }$ and find k.Then write a model that relates y and x. x 5 10 15 20 25 y 26 13

(Multiple Choice)

4.8/5

(32)

Question 40

Exam 10: Mathematical Modeling and Variation

Find a mathematical model representing the statement.(Determine the constant of proportionality. ) ​ Z varies jointly as x and y. (z=128 when x=4 and y=8.)( z = 128 \text { when } x = 4 \text { and } y = 8 . )(z=128 when x=4 and y=8.) ​

After determining whether the variation model below is of the form y=kxy = k xy=kx or y=kxy = \frac { k } { x }y=xk​ ,find the value of k. x 20 40 60 80 100 y

Use the given value of k to complete the table for the direct variation model​ y=kx2y = k x ^ { 2 }y=kx2 . ​ Plot the points on a rectangular coordinate system. x 8 10 12 14 16 y=k k=1

Find a mathematical model representing the statement.(Determine the constant of proportionality. ) ​ Z varies directly as the square of x and inversely as y.(z = 36 when x = 9 and y = 3. ) ​

Determine whether the variation model is of the form y=kxy = k xy=kx or y=kxy = \frac { k } { x }y=xk​ and find k.Then write a model that relates y and x. x 4 8 12 16 20 y 1

Use the given value of k to complete the table for the inverse variation model​ y=kx2y = \frac { k } { x ^ { 2 } }y=x2k​ Plot the points on a rectangular coordinate system. x 2 4 6 8 10 y= k=2

A force of f=225f = 225f=225 newtons stretches a spring s=0.15s = 0.15s=0.15 meter (see figure). How far will a force of 60 newtons stretch the spring? What force is required to stretch the spring 0.1 meter? ​

Assume that y is directly proportional to x.Use the given x-value and y-value to find a linear model that relates y and x.​ x=5,y=24x = 5 , y = 24x=5,y=24 ​

After determining whether the variation model below is of the form y=kxy = k xy=kx or y=kxy = \frac { k } { x }y=xk​ ,find the value of k. x 154 161 168 175 182 y 66 69 72 75 78

Assume that y is directly proportional to x.If x = 28 and y = 21,determine a linear model that relates y and x.

Determine whether the variation model is of the form y=kxy = k xy=kx or y=kxy = \frac { k } { x }y=xk​ and find k.Then write a model that relates y and x. x 9 18 27 36 45 y 2 4 6 8 10

Find a mathematical model representing the statement.(Determine the constant of proportionality. ) ​ Y is inversely proportional to x. (y=7 when x=5.)( y = 7 \text { when } x = 5 . )(y=7 when x=5.) ​

A force of 270 newtons stretches a spring 0.18 meter.What force is required to stretch the spring 0.19 meter? ​

Determine whether the variation model is of the form y=kxy = k xy=kx or y=kxy = \frac { k } { x }y=xk​ and find k.Then write a model that relates y and x. x 5 10 15 20 25 y 26 13

Rectangular Coordinates

Graphs of Equations

Linear Equations in Two Variables

Functions

Analyzing Graphs of Functions

A Library of Parent Functions

Transformations of Functions

Combinations of Functions Composite Functions

Inverse Functions

Quadratic Functions and Models

Polynomial Functions of Higher Degree

Polynomial and Synthetic Division

Complex Numbers

Zeros of Polynomial Functions

Rational Functions

Nonlinear Inequalities

Exponential Functions and Their Graphs

Logarithmic Functions and Their Graphs

Properties of Logarithms

Exponential and Logarithmic Equations

Exponential and Logarithmic Models

Radian and Degree Measure

Trigonometric Functions The Unit Circle

Right Triangle Trigonometry

Trigonometric Functions of Any Angle

Graphs of Sine and Cosine Functions

Graphs of Other Trigonometric Functions

Inverse Trigonometric Functions

Applications and Models

Using Fundamental Identities

Verifying Trigonometric Equations

Solving Trigonometric Equations

Sum and Difference Formulas

Multiple Angle and Product to Sum Formulas

Law of Sines

Law of Cosines

Vectors in the Plane

Vectors and Dot Products

Trigonometric Form of a Complex Number

Linear and Nonlinear Systems of Equations

Two Variable Linear Systems

Multivariable Linear Systems

Partial Fractions

Systems of Inequalities

Linear Programming

Matrices and Systems of Equations

Operations With Matrices

The Inverse of a Square Matrix

The Determinant of a Square Matrix

Applications of Matrices and Determinants

Sequences and Series

Arithmetic Sequences and Partial Sums

Geometric Sequences and Series

Mathematical Induction

The Binomial Theorem

Counting Principles

Probability

Lines

Introduction to Conics Parabolas

Ellipses

Hyperbolas

Rotation of Conics

Parametric Equations

Polar Coordinates

Polar Equations of Conics

Find a mathematical model representing the statement.(Determine the constant of proportionality. ) Z varies jointly as x and y. $( z = 128 \text { when } x = 4 \text { and } y = 8 . )$

After determining whether the variation model below is of the form $y = k x$ or $y = \frac { k } { x }$ ,find the value of k. x 20 40 60 80 100 y

Use the given value of k to complete the table for the direct variation model $y = k x ^ { 2 }$ . Plot the points on a rectangular coordinate system. x 8 10 12 14 16 y=k k=1

Find a mathematical model representing the statement.(Determine the constant of proportionality. ) Z varies directly as the square of x and inversely as y.(z = 36 when x = 9 and y = 3. )

Determine whether the variation model is of the form $y = k x$ or $y = \frac { k } { x }$ and find k.Then write a model that relates y and x. x 4 8 12 16 20 y 1

Use the given value of k to complete the table for the inverse variation model $y = \frac { k } { x ^ { 2 } }$ Plot the points on a rectangular coordinate system. x 2 4 6 8 10 y= k=2

A force of $f = 225$ newtons stretches a spring $s = 0.15$ meter (see figure). How far will a force of 60 newtons stretch the spring? What force is required to stretch the spring 0.1 meter?

Assume that y is directly proportional to x.Use the given x-value and y-value to find a linear model that relates y and x. $x = 5 , y = 24$

After determining whether the variation model below is of the form $y = k x$ or $y = \frac { k } { x }$ ,find the value of k. x 154 161 168 175 182 y 66 69 72 75 78

Determine whether the variation model is of the form $y = k x$ or $y = \frac { k } { x }$ and find k.Then write a model that relates y and x. x 9 18 27 36 45 y 2 4 6 8 10

Find a mathematical model representing the statement.(Determine the constant of proportionality. ) Y is inversely proportional to x. $( y = 7 \text { when } x = 5 . )$

A force of 270 newtons stretches a spring 0.18 meter.What force is required to stretch the spring 0.19 meter?

Determine whether the variation model is of the form $y = k x$ or $y = \frac { k } { x }$ and find k.Then write a model that relates y and x. x 5 10 15 20 25 y 26 13