Exam 17: Process Improvement Using Control Charts

A manufacturer of windows produces one type that has a plastic coating.The specification limits for the plastic coating are 30 and 70.From time to time the plastic coating can become uneven.Therefore,in order to keep the coating as even as possible,thickness measurements are periodically taken at four different locations on the window.15 subgroups were observed and each subgroup consists of the four thickness measurements taken across the windows at a particular time with the following results: mean of the means = 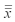= 50.05 and the average range of 8.85. Calculate the control limits for the X-bar chart.

A powder metal manufacturing company is producing sleeves for a locking mechanism.The target (nominal)value for the inside diameter is 1 inch.The inside diameter specifications are 1 $\pm$ .005 inches.Assume that the process is in statistical control with 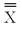= 1.0002 inches, 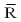= .003 inches and subgroup size of 5. Calculate the control limits for the 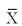chart.

If a process is stable and in statistical control,it is not influenced by assignable causes of variation.

For a manufacturing process, 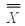= 10 inches, 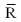= .4 inches and the subgroup sample size is 6 units. Calculate the standard control limits for the 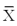chart.

_____ causes of variation may be remedied by local supervision.

A powder metal manufacturing company is producing sleeves for a locking mechanism.The target (nominal)value for the inside diameter is 1 inch.The inside diameter specifications are 1 $\pm$ .005 inches.Assume that the process is in statistical control with 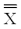= 1.0002 inches, 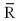= .003 inches and subgroup size of 5. What are the natural tolerance limits for this process? Is the process capable?

If a control chart is used correctly and the necessary corrective actions are taken,then as the control limits get close to each other,the potential quality of the product _____________.

If the process variability steadily increases,we would observe

When a process is influenced only by common causes of variation:

A motorcycle manufacturer produces the parts for its vehicles in different locations and transports them to it plant for assembly.In order to keep the assembly operations running efficiently,it is vital that all parts be within specification limits.One important part used in the assembly is the engine camshaft and one important quality characteristic is the case hardness depth.Specifications state that the hardness depth must be between 3.0 mm and 6.0 mm.To investigate the process,the quality control engineer selected 25 daily subgroups of n = 5 and measured the hardness depth.The process yielded a mean of the means 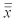= 4.50 and an average range = 1.01. Calculate the center line for the X-bar chart.

Among other quality measures,the quality of an electronic component used in manufacturing stereo speakers is monitored with a p-chart.In the last 25 days daily samples 60 units resulted in the following number of defective units per sample: 8,4,3,7,6,2,5,3,1,0,7,4,2,0,1,6,2,4,3,1,2,8,5,6,0.Determine the center line for this process.

Suppose that 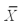and R charts are based on subgroups of size four are being used to monitor the tire diameter size of a new radial tire manufactured by a tire company.The 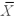and R charts are found to be in statistical control with 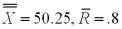inches.A histogram of the tire diameter measurements indicates that distribution of these measurements is approximately normally distributed. Find the sigma level capability of the process.

How well a process is able to meet the requirements set forth by the process design is called the quality of design.

A goal of statistical process control is continuous process improvement.

A manufacturer of windows produces one type that has a plastic coating.The specification limits for the plastic coating are 30 and 70.From time to time the plastic coating can become uneven.Therefore,in order to keep the coating as even as possible,thickness measurements are periodically taken at four different locations on the window.15 subgroups were observed and each subgroup consists of the four thickness measurements taken across the windows at a particular time with the following results: mean of the means = 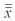= 50.05 and the average range of 8.85. Calculate the center line for the R chart.

Use this information about 10 shipments of light bulbs: If 400 bulbs are selected at random from each of 10 shipments and the number of defectives in each shipment is given above,find the appropriate center line.

In a manufacturing process,if the limits for a control chart are set too _____________,the risk of not investigating a special cause of variation and possibly not taking a corrective action ____________.

A fastener company produces bolts with a nominal (target)length of 2.00 inches.The specifications are 2.00 $\pm$ .006 inches. If the process mean is equal to the target value and the process standard deviation is .0016 determine the value of Cpk.

Observing the output of a process at fixed time intervals is referred to as _____ sampling.

Cause and effect diagram enumerates the potential causes of an undesirable effect on the process to discover sources of process variation and to identify opportunities for process improvement.