Exam 10: Statistical Inferences Based on Two Samples
Exam 1: An Introduction to Business Statistics54 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Methods90 Questions
Exam 3: Descriptive Statistics: Numerical Methods149 Questions
Exam 4: Probability135 Questions
Exam 5: Discrete Random Variables128 Questions
Exam 6: Continuous Random Variables150 Questions
Exam 7: Sampling and Sampling Distributions116 Questions
Exam 8: Confidence Intervals144 Questions
Exam 9: Hypothesis Testing148 Questions
Exam 10: Statistical Inferences Based on Two Samples132 Questions
Exam 11: Experimental Design and Analysis of Variance115 Questions
Exam 12: Chi-Square Tests96 Questions
Exam 13: Simple Linear Regression Analysis148 Questions
Exam 14: Multiple Regression122 Questions
Exam 15: Model Building and Model Diagnostics102 Questions
Exam 16: Time Series Forecasting150 Questions
Exam 17: Process Improvement Using Control Charts122 Questions
Exam 18: Nonparametric Methods97 Questions
Exam 19: Decision Theory90 Questions
Select questions type
In an opinion survey,a random sample of 1000 adults from the U.S.A and 1000 adults from Germany were asked whether they supported the death penalty.590 American adults and 560 German adults indicated that they supported the death penalty.The researcher wants to know if there is sufficient evidence to conclude that the proportion of adults who support the death penalty is higher in the U.S.A.than in Germany.What is the p-value for this test?
(Multiple Choice)
4.8/5  (23)
(23)
When testing H0: 1 - 2 = 2,HA: 1 - 2 > 2,where 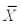 1 = 522,
1 = 522, 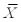 2 = 516, 12 = 28, 22 = 24,n1= 40,n2 = 30,at = .01,what is the test statistic?
2 = 516, 12 = 28, 22 = 24,n1= 40,n2 = 30,at = .01,what is the test statistic?
(Multiple Choice)
4.9/5  (28)
(28)
At 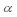 = .10,testing the hypothesis that the proportion of Consumer (CON)industry companies winter quarter profit growth is more than 2% greater than the proportion of Banking (BKG)companies winter quarter profit growth,given that
= .10,testing the hypothesis that the proportion of Consumer (CON)industry companies winter quarter profit growth is more than 2% greater than the proportion of Banking (BKG)companies winter quarter profit growth,given that 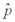 CON= .20,
CON= .20, 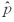 BKG= .14,nCON = 300,nBKG = 400,calculate the estimated standard deviation for the model.
BKG= .14,nCON = 300,nBKG = 400,calculate the estimated standard deviation for the model.
(Multiple Choice)
4.8/5  (26)
(26)
In an experiment involving matched pairs,a sample of 12 pairs of observations is collected.The degree of freedom for the t statistic is 10.
(True/False)
4.8/5  (34)
(34)
Find a 95 percent confidence interval for µ1- µ2,where n1= 50,n2 = 75, 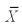 1 = 82,
1 = 82, 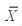 2 = 76, 12 = 8 and 22 = 6.
2 = 76, 12 = 8 and 22 = 6.
(Multiple Choice)
5.0/5  (34)
(34)
In testing the difference between the means of two normally distributed populations using large,independent random samples with known variances,the correct test statistic to use is:
(Multiple Choice)
4.8/5  (22)
(22)
Let p1 represent the population proportion of U.S.Senate and Congress (House of Representatives)democrats who are in favor of a new modest tax on "junk food".Let p2 represent the population proportion of U.S.Senate and Congress (House of Representative)republicans who are in favor of a new modest tax on "junk food".Out of the 265 democratic senators and congressman 106 of them are in favor of a "junk food" tax.Out of the 285 republican senators and congressman only 57 of them are in favor of a "junk food" tax.At 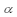 = .01,can we conclude that the proportion of democrats who favor "junk food" tax is more than 5% higher than proportion of republicans who favor the new tax?
= .01,can we conclude that the proportion of democrats who favor "junk food" tax is more than 5% higher than proportion of republicans who favor the new tax?
(Multiple Choice)
4.8/5  (33)
(33)
The registrar at a state college is interested in determining whether there is a difference of more than one credit hour between male and female students in the average number of credit hours taken during a term.She selected a random sample of 60 male and 60 female students and observed the following sample information. 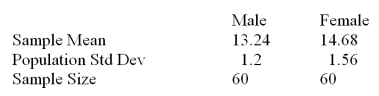 What do you conclude if z = 1.73 at = .01?
What do you conclude if z = 1.73 at = .01?
(Multiple Choice)
5.0/5  (37)
(37)
Two hospital emergency rooms use different procedures for triage of their patients.We want to test the claim that the mean waiting time of patients is the same for both hospitals.The 40 randomly selected subjects from one hospital produce a mean of 18.3 minutes.The 50 randomly selected patients from the other hospital produce a mean of 25.31 minutes.Assume a a = 2.1 minutes and b = 2.92 minutes.What do you conclude about the waiting time for patients in the two hospitals testing at = .001?
(Multiple Choice)
4.8/5  (30)
(30)
If we are testing the hypothesis about the mean of a population of paired differences with samples of n1 = 10,n2 = 10,the degrees of freedom for the t statistic is ____.
(Multiple Choice)
4.9/5  (30)
(30)
A test of spelling ability is given to a random sample of 10 students before and after they completed a spelling course.The mean score before the course was 119.60 and after the course the mean score was 130.80.The standard deviation of the difference was 16.061.Test the hypothesis at 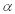 = .05
= .05
(Multiple Choice)
4.9/5  (35)
(35)
Calculate the t statistic for testing equality of means where 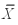 1 = 8.2,
1 = 8.2, 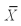 2 = 11.3,s12 = 5.4,s22 = 5.2,n1= 6,n2 = 7.(Assume equal population variances)
2 = 11.3,s12 = 5.4,s22 = 5.2,n1= 6,n2 = 7.(Assume equal population variances)
(Multiple Choice)
4.9/5  (31)
(31)
In testing the equality of population variances,two assumptions are required: independent samples and normally distributed populations.
(True/False)
4.8/5  (34)
(34)
In an opinion survey,a random sample of 1000 adults from the U.S.A and 1000 adults from Germany were asked whether they supported the death penalty.590 American adults and 560 German adults indicated that they supported the death penalty.The researcher wants to know if there is sufficient evidence to conclude that the proportion of adults who support the death penalty is higher in the U.S.A.than in Germany.What is the rejection point (critical value of the test statistic)at 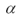 = .05?
= .05?
(Multiple Choice)
4.9/5  (38)
(38)
Given two independent normal distributions with s12- s12 = 100,µ1= µ2 = 50,n1= n2 = 50,the sampling distribution of the mean difference 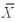 1-
1- 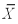 2 will have a mean of _________.
2 will have a mean of _________.
(Multiple Choice)
4.8/5  (41)
(41)
When testing the difference between two proportions selected from populations with large independent samples,the Z test statistic is used.
(True/False)
4.9/5  (38)
(38)
In order to test the effectiveness of a drug called XZR designed to reduce cholesterol levels,9 heart patients' cholesterol levels are measured before they are given the drug.The same 9 patients use XZR for two continuous months.After two months of continuous use the 9 patients' cholesterol levels are measured again.The comparison of cholesterol levels before vs.after administering the drug is an example of testing the difference between:
(Multiple Choice)
4.7/5  (27)
(27)
In testing for the equality of means from two independent populations,if the null hypothesis is rejected,the test could result in:
(Multiple Choice)
4.9/5  (35)
(35)
In testing the difference between the means of two independent populations,if neither population is normally distributed,then the sampling distribution of the difference in means will be approximately normal provided that the sum of the sample sizes obtained from the two populations are at least 30.
(True/False)
4.9/5  (36)
(36)
Find a 95 percent confidence interval for µ1- µ2,where n1= 15,n2 = 10, 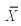 1 = 1.94,
1 = 1.94, 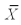 2 = 1.04,s12 = .2025 and s22 = .0676.(Assume equal population variances)
2 = 1.04,s12 = .2025 and s22 = .0676.(Assume equal population variances)
(Multiple Choice)
4.9/5  (34)
(34)
Showing 61 - 80 of 132
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)