Exam 16: Vector Calculus
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Show that F is conservative, and find a function f such that 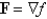 , and use the result to evaluate
, and use the result to evaluate 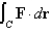 , where C is any curve from
, where C is any curve from 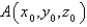 to
to 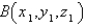 .
. 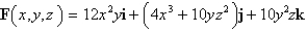 ;
; 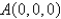 and
and 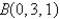
(Multiple Choice)
4.7/5  (29)
(29)
A particle starts at the point 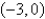 , moves along the x-axis to (3, 0) and then along the semicircle
, moves along the x-axis to (3, 0) and then along the semicircle 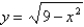 to the starting point. Use Green's Theorem to find the work done on this particle by the force field
to the starting point. Use Green's Theorem to find the work done on this particle by the force field 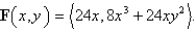
(Multiple Choice)
4.7/5  (32)
(32)
Evaluate 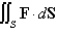 , that is, find the flux of F across S.
, that is, find the flux of F across S. 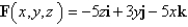 ; S is the hemisphere
; S is the hemisphere 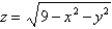 ; n points upward.
; n points upward.
(Multiple Choice)
4.7/5  (40)
(40)
Use Stokes' Theorem to evaluate 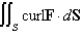 .
. 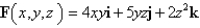 ;
S is the part of the ellipsoid
;
S is the part of the ellipsoid 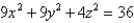 lying above the xy-plane and oriented with normal pointing upward.
lying above the xy-plane and oriented with normal pointing upward.
(Short Answer)
4.9/5  (34)
(34)
Evaluate 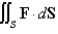 , that is, find the flux of F across S.
, that is, find the flux of F across S. 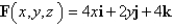 ; S is the part of the paraboloid
; S is the part of the paraboloid 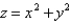 between the planes z = 0 and z = 5; n points upward.
between the planes z = 0 and z = 5; n points upward.
(Essay)
4.9/5  (36)
(36)
Find the area of the surface S where S is the part of the surface 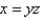 that lies inside the cylinder
that lies inside the cylinder 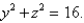
(Essay)
4.8/5  (42)
(42)
Evaluate 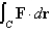 for the vector field F and the path C. (Hint: Show that F is conservative, and pick a simpler path.)
for the vector field F and the path C. (Hint: Show that F is conservative, and pick a simpler path.) 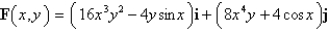 C:
C: 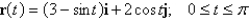
(Multiple Choice)
4.7/5  (35)
(35)
Find the mass of the surface S having the given mass density. S is the hemisphere 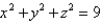 ,
, 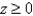 ; the density at a point P on S is equal to the distance between P and the xy-plane.
; the density at a point P on S is equal to the distance between P and the xy-plane.
(Multiple Choice)
4.8/5  (35)
(35)
The plot of a vector field is shown below. A particle is moved 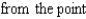
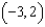

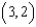 . By inspection, determine whether the work done by F on the particle is positive, negative, or zero.
. By inspection, determine whether the work done by F on the particle is positive, negative, or zero. 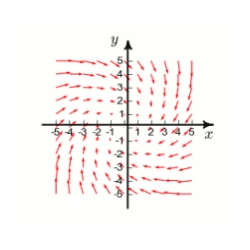
(Short Answer)
4.8/5  (38)
(38)
Determine whether or not vector field is conservative. If it is conservative, find a function f such that 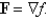
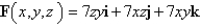
(Essay)
4.8/5  (42)
(42)
Use Green's Theorem to evaluate the line integral along the positively oriented closed curve C. 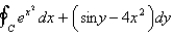 , where C is the boundary of the region bounded by the parabolas
, where C is the boundary of the region bounded by the parabolas 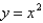 and
and 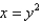 .
.
(Multiple Choice)
4.9/5  (43)
(43)
Find the work done by the force field F on a particle that moves along the curve C. 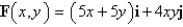 ;
; 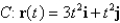 ,
, 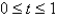
(Multiple Choice)
4.8/5  (34)
(34)
Find the area of the surface. The part of the paraboloid 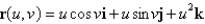 ;
; 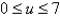 ,
, 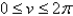
(Multiple Choice)
4.8/5  (32)
(32)
Use Stokes' Theorem to evaluate 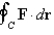 .
. 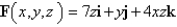 ;
C is the boundary of the triangle with vertices
;
C is the boundary of the triangle with vertices 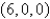 ,
, 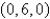 , and
, and 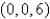 oriented in a counterclockwise direction when viewed from above
oriented in a counterclockwise direction when viewed from above
(Short Answer)
4.9/5  (27)
(27)
Find an equation in rectangular coordinates, and then identify the surface. 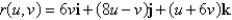
(Essay)
4.8/5  (49)
(49)
Assuming that S satisfies the conditions of the Divergence Theorem and the scalar functions and components of the vector fields have continuous second order partial derivatives, find 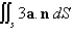 , where a is the constant vector.
, where a is the constant vector.
(Multiple Choice)
4.8/5  (30)
(30)
Showing 61 - 80 of 137
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)