Exam 16: Vector Calculus
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Use a computer algebra system to compute the flux of F across S. S is the surface of the cube cut from the first octant by the planes 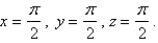
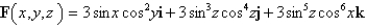
(Multiple Choice)
5.0/5  (37)
(37)
A particle is moving in a velocity field 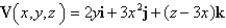 At time t = 1 the particle is located at the point (1, 5, 5).
a). What is the velocity of the particle at t = 1?
b). What is the approximate location of the particle at t = 1.01?
At time t = 1 the particle is located at the point (1, 5, 5).
a). What is the velocity of the particle at t = 1?
b). What is the approximate location of the particle at t = 1.01?
(Essay)
4.9/5  (46)
(46)
Use Gauss's Law to find the charge contained in the solid hemisphere 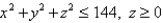 , if the electric field is
, if the electric field is 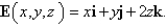
(Essay)
4.8/5  (38)
(38)
Find an equation of the tangent plane to the parametric surface represented by r at the specified point. 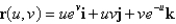 ; u = ln 5, v = 0
; u = ln 5, v = 0
(Essay)
4.8/5  (40)
(40)
Find the gradient vector field of the scalar function f (That is, find the conservative vector field F for the potential function f of F.) 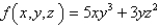
(Multiple Choice)
4.8/5  (41)
(41)
Use Stokes' Theorem to evaluate 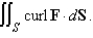
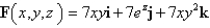 S consists of the four sides of the pyramid with vertices (0, 0, 0), (3, 0, 0), (0, 0, 3), (3, 0,3) and (0, 3, 0) that lie to the right of the xz-plane, oriented in the direction of the positive y-axis.
S consists of the four sides of the pyramid with vertices (0, 0, 0), (3, 0, 0), (0, 0, 3), (3, 0,3) and (0, 3, 0) that lie to the right of the xz-plane, oriented in the direction of the positive y-axis.
(Multiple Choice)
4.9/5  (36)
(36)
Find the work done by the force field F on a particle that moves along the curve C. 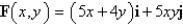 ;
; 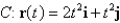 ,
, 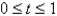
(Multiple Choice)
4.9/5  (37)
(37)
Find the value of the constant c such that the vector field 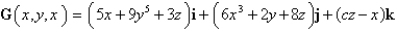 is the curl of some vector field F.
is the curl of some vector field F.
(Multiple Choice)
4.9/5  (33)
(33)
Determine whether F is conservative. If so, find a function f such that 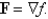 .
. 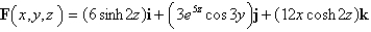
(Essay)
4.9/5  (33)
(33)
Find the moment of inertia about the z-axis of a thin funnel in the shape of a cone 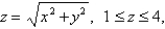 if its density function is
if its density function is 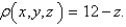
(Essay)
4.9/5  (41)
(41)
Find the area of the surface S where S is the part of the sphere 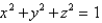 that lies inside the cylinder
that lies inside the cylinder 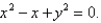
(Essay)
4.8/5  (36)
(36)
Evaluate the line integral over the given curve C. 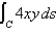 , where C is the line segment joining (-4, -5) to (5, 4)
, where C is the line segment joining (-4, -5) to (5, 4)
(Essay)
4.7/5  (47)
(47)
Let F be a vector field. Determine whether the expression is meaningful. If so, state whether the expression represents a scalar field or a vector field. 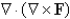
(Essay)
4.9/5  (38)
(38)
Use Stoke's theorem to evaluate 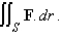
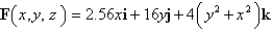 C is the boundary of the part of the paraboloid
C is the boundary of the part of the paraboloid 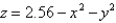 in the first octant. C is oriented counterclockwise as viewed from above.
in the first octant. C is oriented counterclockwise as viewed from above.
(Short Answer)
4.8/5  (31)
(31)
Determine whether or not F is a conservative vector field. If it is, find a function f such that 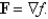
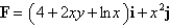
(Essay)
4.9/5  (45)
(45)
Determine whether F is conservative. If so, find a function f such that 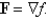 .
. 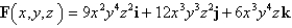
(Essay)
4.9/5  (34)
(34)
Showing 81 - 100 of 137
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)