Exam 16: Vector Calculus
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Find a parametric representation for the part of the elliptic paraboloid 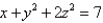 that lies in front of the plane x = 0.
that lies in front of the plane x = 0.
(Multiple Choice)
4.7/5  (44)
(44)
Evaluate 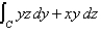 , where C is given by
, where C is given by 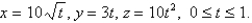 Round your answer to two decimal place.
Round your answer to two decimal place.
(Multiple Choice)
4.8/5  (34)
(34)
Use Green's Theorem to find the work done by the force 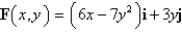 in moving a particle in the positive direction once around the triangle with vertices
in moving a particle in the positive direction once around the triangle with vertices 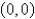 ,
, 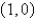 , and
, and 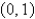 .
.
(Multiple Choice)
4.9/5  (31)
(31)
Use Green's Theorem to evaluate the line integral along the given positively oriented curve. 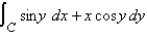 C is the ellipse
C is the ellipse 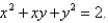
(Short Answer)
4.9/5  (39)
(39)
Determine whether F is conservative. If so, find a function f such that 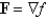 .
. 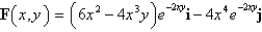
(Multiple Choice)
4.8/5  (32)
(32)
Let S be the cube with vertices 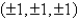 . Approximate
. Approximate 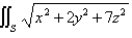 by using a Riemann sum as in Definition 1, taking the patches
by using a Riemann sum as in Definition 1, taking the patches 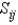 to be the squares that are the faces of the cube and the points
to be the squares that are the faces of the cube and the points 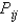 to be the centers of the squares.
to be the centers of the squares.
(Multiple Choice)
4.9/5  (25)
(25)
A thin wire in the shape of a quarter-circle 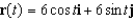 ,
, 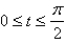 , has a linear mass density
, has a linear mass density 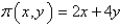 . Find the mass and the location of the center of mass of the wire.
. Find the mass and the location of the center of mass of the wire.
(Essay)
4.9/5  (38)
(38)
The temperature at the point 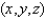 in a substance with conductivity
in a substance with conductivity 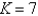 is
is 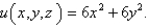 Find the rate of heat flow inward across the cylindrical
Find the rate of heat flow inward across the cylindrical 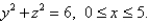
(Multiple Choice)
4.7/5  (42)
(42)
Let D be a region bounded by a simple closed path C in the xy. Then the coordinates of the centroid 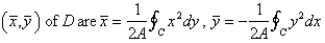 where A is the area of D. Find the centroid of the triangle with vertices (0, 0), (
where A is the area of D. Find the centroid of the triangle with vertices (0, 0), ( 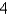 , 0) and (0,
, 0) and (0, 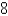 ).
).
(Multiple Choice)
4.8/5  (30)
(30)
Use Stoke's theorem to calculate the surface integral 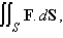 where
where 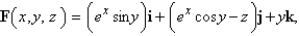 and S is the part of the cone
and S is the part of the cone 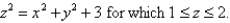
(Short Answer)
4.8/5  (31)
(31)
Find a function f such that 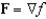 and use it to evaluate
and use it to evaluate 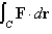 along the given curve C.
along the given curve C. 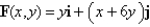 C is the upper semicircle that starts at (1, 2) and ends at (5, 2).
C is the upper semicircle that starts at (1, 2) and ends at (5, 2).
(Short Answer)
4.8/5  (42)
(42)
Determine whether or not F is a conservative vector field. If it is, find a function f such that 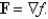
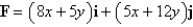 .
.
(Essay)
4.8/5  (36)
(36)
A plane lamina with constant density 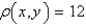 occupies a region in the xy-plane bounded by a simple closed path C. Its moments of inertia about the axes are
occupies a region in the xy-plane bounded by a simple closed path C. Its moments of inertia about the axes are 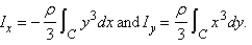 Find the moments of inertia about the axes, if C is a rectangle with vertices (0, 0), (4, 0), (4, 5) and
Find the moments of inertia about the axes, if C is a rectangle with vertices (0, 0), (4, 0), (4, 5) and 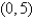 .
.
(Multiple Choice)
4.8/5  (35)
(35)
Evaluate 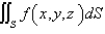 .
. 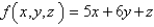 ; S is the part of the cone
; S is the part of the cone 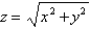 between the planes
between the planes 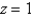 and
and 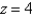 .
.
(Multiple Choice)
4.8/5  (31)
(31)
Use Stokes' Theorem to evaluate 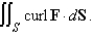 S consists of the top and the four sides (but not the bottom) of the cube with vertices
S consists of the top and the four sides (but not the bottom) of the cube with vertices 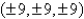 oriented outward.
oriented outward. 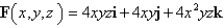
(Short Answer)
4.9/5  (39)
(39)
Showing 121 - 137 of 137
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)