Exam 3: Applications of Differentiation
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
A rectangular box having a top and a square base is to be constructed at a cost of $1. If the material for the bottom costs $0.35 per square foot, the material for the top costs $0.15 per square foot, and the material for the sides costs $0.20 per square foot, find the dimensions and volume of the box of maximum volume that can be constructed.
(Essay)
4.9/5  (27)
(27)
For what values of c does the curve have maximum and minimum points? 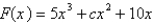
(Multiple Choice)
4.8/5  (33)
(33)
The quantity demanded per month of an item is related to the unit price by the demand equation 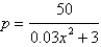 ,
, 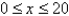 where p is measured in dollars and x is measured in units of a thousand. How many items must be sold by the manufacturer to maximize its revenue? Hint: Recall that the revenue is given by
where p is measured in dollars and x is measured in units of a thousand. How many items must be sold by the manufacturer to maximize its revenue? Hint: Recall that the revenue is given by 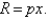
(Short Answer)
4.8/5  (35)
(35)
Find the absolute maximum and absolute minimum values, if any, of the function 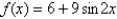 on
on  .
.
(Multiple Choice)
4.8/5  (34)
(34)
An efficiency study showed that the total number of cell phones assembled by the average worker at a manufacturing company t hours after starting work at 8 a.m.is given by 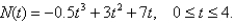 Sketch the graph of the function N, and interpret your result.
Sketch the graph of the function N, and interpret your result.
(Essay)
4.9/5  (30)
(30)
A production editor decided that a promotional flyer should have a 1-in. margin at the top and the bottom, and a 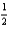 -in. margin on each side. The editor further stipulated that the flyer should have an area of 288
-in. margin on each side. The editor further stipulated that the flyer should have an area of 288 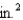 . Determine the dimensions of the flyer that will result in the maximum printed area on the flyer.
. Determine the dimensions of the flyer that will result in the maximum printed area on the flyer. 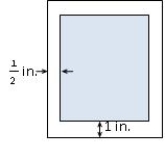
(Multiple Choice)
4.9/5  (34)
(34)
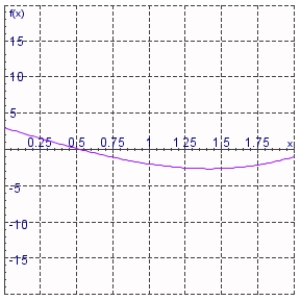
Estimate the absolute minimum value of the function 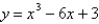 to two decimal places on the interval
to two decimal places on the interval 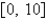 .
. 
(Essay)
4.8/5  (37)
(37)
Find the slant asymptote of the graph of 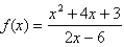 using the curve-sketching guidelines.
using the curve-sketching guidelines.
(Multiple Choice)
4.9/5  (26)
(26)
Determine where the graph of the function 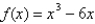 is concave upward and where it is concave downward. Also, find all inflection points of the function.
is concave upward and where it is concave downward. Also, find all inflection points of the function.
(Multiple Choice)
4.7/5  (35)
(35)
Find the dimensions of the rectangle enclosed in the semicircle 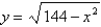 with the largest possible area.
with the largest possible area. 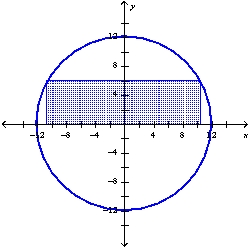
(Multiple Choice)
4.8/5  (32)
(32)
The graph of the second derivative 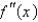 of a function f is shown. State the x-coordinates of the inflection points of
f.
of a function f is shown. State the x-coordinates of the inflection points of
f. 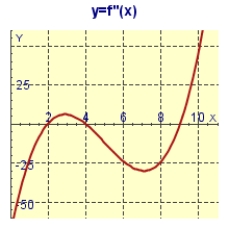
(Short Answer)
4.8/5  (31)
(31)
A car braked with a constant deceleration of 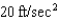 , producing skid marks measuring 500 ft before coming to a stop. How fast was the car traveling when the brakes were first applied?
, producing skid marks measuring 500 ft before coming to a stop. How fast was the car traveling when the brakes were first applied?
(Short Answer)
4.9/5  (34)
(34)
Given that the graph of f passes through the point (4, 69) and that the slope of its tangent line at 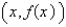 is
is 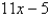 , find f (1) .
, find f (1) .
(Multiple Choice)
4.9/5  (30)
(30)
Showing 41 - 60 of 153
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)