Exam 3: Applications of Differentiation
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Sketch the graph of the function 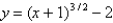 using the curve-sketching guidelines.
using the curve-sketching guidelines.
(Multiple Choice)
4.9/5  (30)
(30)
The graph of the derivative 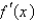 of a continuous function f is shown. On what intervals is f decreasing?
of a continuous function f is shown. On what intervals is f decreasing?  .
.
(Multiple Choice)
5.0/5  (34)
(34)
You are given the graph of a function f. Determine the intervals where the graph of f is concave upward and where it is concave downward.Find all inflection points of f.
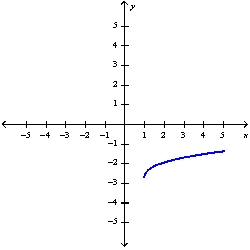
(Essay)
4.9/5  (33)
(33)
You are given the graph of the second derivative 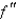 of a function f.
of a function f.
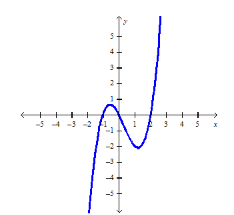 (a) Determine the intervals where the graph of f is concave upward and where it is concave downward.(b) Find the x-coordinates all inflection points of f.
(a) Determine the intervals where the graph of f is concave upward and where it is concave downward.(b) Find the x-coordinates all inflection points of f.
(Essay)
4.9/5  (45)
(45)
A rectangular beam will be cut from a cylindrical log of radius 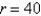 inches. Suppose that the strength of a rectangular beam is proportional to the product of its width and the square of its depth. Find the dimensions of the strongest beam that can be cut from the cylindrical log.
inches. Suppose that the strength of a rectangular beam is proportional to the product of its width and the square of its depth. Find the dimensions of the strongest beam that can be cut from the cylindrical log. 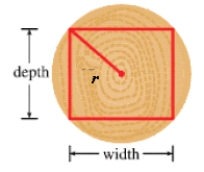
(Multiple Choice)
4.9/5  (30)
(30)
Determine where the graph of the function 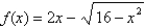 is concave upward and where it is concave downward. Also, find all inflection points of the function.
is concave upward and where it is concave downward. Also, find all inflection points of the function.
(Multiple Choice)
4.9/5  (30)
(30)
How many real roots does the equation 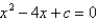 have in the interval
have in the interval 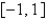 ?
?
(Multiple Choice)
4.7/5  (43)
(43)
Estimate the value of 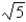 by using three iterations of Newton's method to solve the equation
by using three iterations of Newton's method to solve the equation 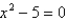 with initial estimate
with initial estimate 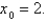 Round your final estimate to four decimal places.
Round your final estimate to four decimal places.
(Multiple Choice)
4.8/5  (29)
(29)
Find the local and absolute extreme values of the function on the given interval. 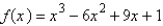 ,
, 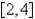
(Essay)
4.9/5  (29)
(29)
Find the position function of a particle moving along a coordinate line that satisfies the given conditions. 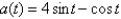 , s(0) = 5, v(0) = 0
, s(0) = 5, v(0) = 0
(Essay)
4.9/5  (40)
(40)
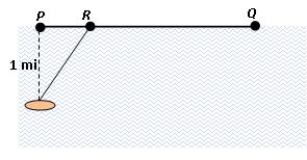
A woman is on a lake in a rowboat located one mile form the closest point P of a straight shoreline (see the figure). She wishes to get to point Q, 8 miles along the shore from P, by rowing to a point R between P and Q and then walking the rest of the distance. If she can row at a speed of 3 mph and walk at a speed of 4 mph, how should she pick the point R to get to Q as quickly as possible? How much time does she require?
 8 mi
8 mi 
(Essay)
4.9/5  (37)
(37)
A Norman window has the shape of a rectangle surmounted by a semicircle. (Thus the diameter of the semicircle is equal to the width of the rectangle.) If the perimeter of the window is 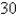 ft, find the dimensions of the window so that the greatest possible amount of light is admitted.
ft, find the dimensions of the window so that the greatest possible amount of light is admitted.
(Essay)
4.8/5  (30)
(30)
A steel pipe is being carried down a hallway 14 ft wide. At the end of the hall there is a right-angled turn into a narrower hallway 6 ft wide. What is the length of the longest pipe that can be carried horizontally around the corner? 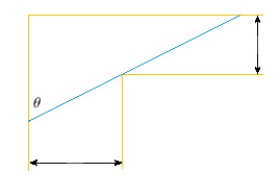
(Short Answer)
5.0/5  (38)
(38)
Find the dimensions of a rectangle of area 400 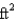 that has the smallest possible perimeter.
that has the smallest possible perimeter.
(Multiple Choice)
4.8/5  (24)
(24)
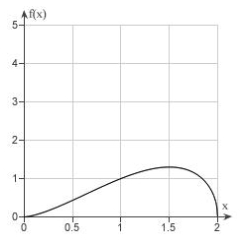
Estimate the absolute maximum value of the function 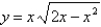 to two decimal places on the interval
to two decimal places on the interval 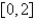 .
. 
(Short Answer)
4.9/5  (36)
(36)
The function 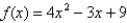 satisfies the hypotheses of the Mean Value Theorem on the interval
satisfies the hypotheses of the Mean Value Theorem on the interval 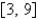 . Find all values of c that satisfy the conclusion of the theorem.
. Find all values of c that satisfy the conclusion of the theorem.
(Multiple Choice)
4.8/5  (36)
(36)
Showing 121 - 140 of 153
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)