Exam 3: Applications of Differentiation
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Suppose the line 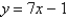 is tangent to the curve
is tangent to the curve 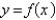 when
when 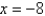 . If Newton's method is used to locate a root of the equation
. If Newton's method is used to locate a root of the equation 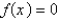 and the initial approximation is
and the initial approximation is 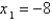 , find the second approximation
, find the second approximation 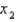 .
.
(Essay)
4.8/5  (36)
(36)
Sketch the graph of the function 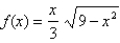 using the curve-sketching guidelines.
using the curve-sketching guidelines.
(Multiple Choice)
4.9/5  (39)
(39)
The graph of the derivative 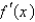 of a continuous function f is shown. On what intervals is f decreasing?
of a continuous function f is shown. On what intervals is f decreasing? 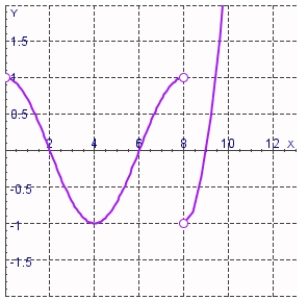
(Essay)
4.7/5  (33)
(33)
Verify that the function satisfies the three hypotheses of Rolle's Theorem on the given interval. Then find all numbers c that satisfy the conclusion of Rolle's Theorem. 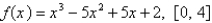
(Multiple Choice)
4.8/5  (39)
(39)
Given 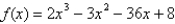 . (a) Find the intervals on which f is increasing or decreasing. (b) Find the relative maxima and relative minima of F.
. (a) Find the intervals on which f is increasing or decreasing. (b) Find the relative maxima and relative minima of F.
(Multiple Choice)
4.9/5  (37)
(37)
The sum of two positive numbers is 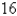 . What is the smallest possible value of the sum of their squares?
. What is the smallest possible value of the sum of their squares?
(Essay)
4.7/5  (31)
(31)
Use Newton's method to approximate the zero of 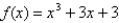 between
between 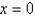 and
and 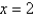 using
using 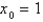 . Continue until two successive approximations differ by less than 0.00001.
. Continue until two successive approximations differ by less than 0.00001.
(Short Answer)
4.9/5  (32)
(32)
Given 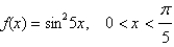 .
(a) Find the intervals on which f is increasing or decreasing.
(b) Find the relative maxima and relative minima of f.
.
(a) Find the intervals on which f is increasing or decreasing.
(b) Find the relative maxima and relative minima of f.
(Essay)
4.9/5  (36)
(36)
The graph of the first derivative  of a function f is shown below. At what values of x does f have a local maximum or minimum?
of a function f is shown below. At what values of x does f have a local maximum or minimum? 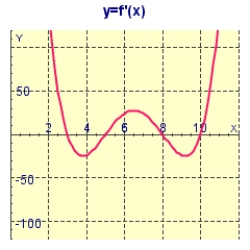
(Short Answer)
4.7/5  (35)
(35)
Find the position function of a particle moving along a coordinate line that satisfies the given condition. 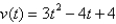 , s(1) = -1
, s(1) = -1
(Essay)
4.8/5  (33)
(33)
Sketch the graph of the function 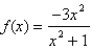 using the curve-sketching guidelines.
using the curve-sketching guidelines.
(Essay)
4.7/5  (38)
(38)
Let f (x) = 4x3 - 5x2 + x - 2 and g (x) = 4x3
a.Plot the graph of f and g using the same viewing window: [-5, 5] ´ [-5, 5].
b.Plot the graph of f and g using the same viewing window: [-50, 50] ´ [-100,000, 100,000]
c.Explain why the graphs of f and g that you obtained in part (b) seem coalesce as x increases or decreases without bound.
(Essay)
4.9/5  (33)
(33)
Sketch the graph of 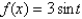 on
on 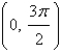 and find its absolute maximum and absolute minimum values, if any.
and find its absolute maximum and absolute minimum values, if any.
(Essay)
4.8/5  (29)
(29)
What is the shortest possible length of the line segment that is cut off by the first quadrant and is tangent to the curve 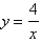 at some point?
at some point?
(Multiple Choice)
4.9/5  (28)
(28)
Determine where the graph of the function 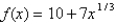 is concave upward and where it is concave downward. Also, find all inflection points of the function.
is concave upward and where it is concave downward. Also, find all inflection points of the function.
(Multiple Choice)
4.8/5  (34)
(34)
The function 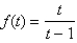 satisfies the hypotheses of the Mean Value Theorem on the interval
satisfies the hypotheses of the Mean Value Theorem on the interval 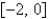 . Find all values of c that satisfy the conclusion of the theorem.
. Find all values of c that satisfy the conclusion of the theorem.
(Essay)
4.8/5  (31)
(31)
A company estimates that the marginal cost (in dollars per item) of producing items is 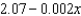 . If the cost of producing one item is $560 find the cost of producing 400 items.
. If the cost of producing one item is $560 find the cost of producing 400 items.
(Essay)
4.7/5  (40)
(40)
Showing 81 - 100 of 153
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)