Exam 3: Applications of Differentiation
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Use Newton's method to approximate the indicated root of 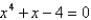 in the interval
in the interval 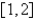 , correct to six decimal places.
Use
, correct to six decimal places.
Use 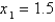 as the initial approximation.
as the initial approximation.
(Short Answer)
4.9/5  (37)
(37)
A skydiver leaps from a helicopter hovering high above the ground. Her velocity t sec later and before deploying her parachute is given by 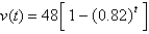 where
where 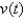 is measured in meters per second. What is her terminal velocity? Hint: Evaluate
is measured in meters per second. What is her terminal velocity? Hint: Evaluate 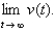
(Multiple Choice)
4.8/5  (34)
(34)
The altitude (in feet) attained by a model rocket t sec into flight is given by the function 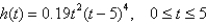 .
When is the rocket ascending, and when is it descending? What is the maximum altitude attained by the rocket?
.
When is the rocket ascending, and when is it descending? What is the maximum altitude attained by the rocket?
(Essay)
4.8/5  (46)
(46)
Find a cubic function 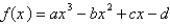 that has a local maximum value of 112 at 1 and a local minimum value of -1,184 at 7.
that has a local maximum value of 112 at 1 and a local minimum value of -1,184 at 7.
(Essay)
4.9/5  (31)
(31)
Sketch the graph of the function 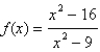 using the curve-sketching guidelines.
using the curve-sketching guidelines.
(Essay)
4.7/5  (39)
(39)
Use Newton's method to find the point of intersection of the graphs of 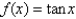 and
and 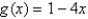 to within 0.00001 by solving the equation
to within 0.00001 by solving the equation 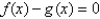 using
using 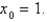
(Short Answer)
4.8/5  (35)
(35)
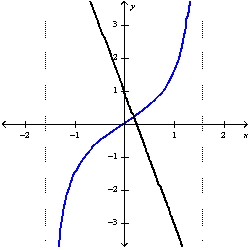
Use Newton's method to approximate the zero of 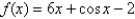 between
between 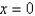 and
and 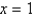 using
using 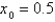 . Continue until two successive approximations differ by less than 0.00001.
. Continue until two successive approximations differ by less than 0.00001.
(Multiple Choice)
4.9/5  (28)
(28)
What constant acceleration is required to increase the speed of a car from 30 ft/s to 45 ft/s in
4 s?
(Essay)
4.7/5  (42)
(42)
Sketch the graph of the function 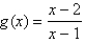 using the curve-sketching guidelines.
using the curve-sketching guidelines.
(Multiple Choice)
5.0/5  (38)
(38)
A woman at a point A on the shore of a circular lake with radius 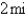 wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time. She can walk at the rate of
wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time. She can walk at the rate of 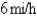 and row a boat at
and row a boat at 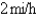 . How should she proceed? (Find
. How should she proceed? (Find 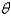 ). Round the result, if necessary, to the nearest hundredth.
). Round the result, if necessary, to the nearest hundredth. 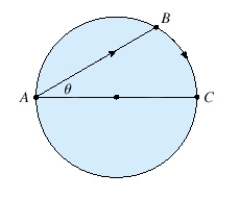
(Multiple Choice)
4.9/5  (40)
(40)
Showing 21 - 40 of 153
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)