Exam 15: Multiple Integrals
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Find the volume of the solid bounded in the first octanat bounded by the cylinder and the planes .
(Short Answer)
4.9/5  (32)
(32)
Find the mass and the center of mass of the lamina occupying the region R, where R is the region bounded by the graphs of the equations and and having the mass density
(Short Answer)
4.9/5  (28)
(28)
Use a double integral to find the area of the region R where R is bounded by the circle
(Multiple Choice)
4.9/5  (38)
(38)
Evaluate the double integral , where is the triangular region with vertices and .
(Short Answer)
4.9/5  (29)
(29)
Find the center of mass of the lamina of the region shown if the density of the circular lamina is four times that of the rectangular lamina. 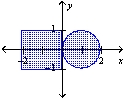
(Short Answer)
4.8/5  (25)
(25)
An electric charge is spread over a rectangular region Find the total charge on R if the charge density at a point in R (measured in coulombs per square meter) is
(Multiple Choice)
4.7/5  (37)
(37)
Sketch the solid whose volume is given by the integral Evaluate the integral.
(Short Answer)
4.9/5  (37)
(37)
Evaluate the integral , where R is the annular region bounded by the circles and by changing to polar coordinates.
(Short Answer)
4.9/5  (27)
(27)
Find the area of the surface. The part of the sphere that lies above the plane .
(Multiple Choice)
4.7/5  (39)
(39)
Evaluate the double integral. , is triangular region with vertices .
(Short Answer)
4.7/5  (30)
(30)
Find the area of the surface S where S is the part of the surface that lies inside the cylinder
(Short Answer)
4.9/5  (30)
(30)
Use cylindrical coordinates to evaluate where E is the region that lies inside the cylinder and between the planes . Round the answer to two decimal places.
(Multiple Choice)
4.9/5  (28)
(28)
Use cylindrical or spherical coordinates, whichever seems more appropriate, to evaluate where E lies above the paraboloid and below the plane .
(Multiple Choice)
4.9/5  (30)
(30)
Find the area of the surface. The part of the surface that lies above the xy-plane.
(Multiple Choice)
4.8/5  (31)
(31)
Find the center of mass of the system comprising masses mk located at the points Pk in a coordinate plane. Assume that mass is measured in grams and distance is measured in centimeters.
m1 = 4, m2 = 3, m3 = 2
P1(-3, -3), P2(0, 3), P3(-2, -1)
(Short Answer)
5.0/5  (41)
(41)
Use cylindrical coordinates to evaluate where T is the solid bounded by the cylinder and the planes and
(Multiple Choice)
5.0/5  (29)
(29)
Showing 21 - 40 of 124
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)