Exam 14: Partial Derivatives
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
The ellipsoid intersects the plane in an ellipse. Find parametric equations for the tangent line to this ellipse at the point (1, 2, 2).
(Multiple Choice)
4.7/5  (33)
(33)
Find the equation of the normal line to the given surface at the specified point.
(Multiple Choice)
4.8/5  (37)
(37)
The height of a hill (in feet) is given by where x is the distance (in miles) east and y is the distance (in miles) north of your cabin. If you are at a point on the hill 1 mile north and 1 mile east of your cabin, what is the rate of change of the height of the hill (a) in a northerly direction and (b) in an easterly direction?
(Multiple Choice)
4.9/5  (33)
(33)
Find the directional derivative of at the point (1, 3) in the direction toward the point (3, 1). Select the correct answer.
(Multiple Choice)
4.9/5  (33)
(33)
Use Lagrange multipliers to find the maximum and the minimum of f subject to the given constraint(s).
(Short Answer)
4.8/5  (35)
(35)
Find three positive real numbers whose sum is 388 and whose product is as large as possible.
(Short Answer)
4.9/5  (35)
(35)
A cardboard box without a lid is to have a volume of cm . Find the dimensions that minimize the amount of cardboard used.
(Short Answer)
4.8/5  (40)
(40)
Find three positive numbers whose sum is and whose product is a maximum.
(Short Answer)
4.8/5  (32)
(32)
Use differentials to estimate the amount of metal in a closed cylindrical can that is 12 cm high and 8 cm in diameter if the metal in the top and bottom is 0.09 cm thick and the metal in the sides is 0.01 cm thick. (rounded to the nearest hundredth.)
(Multiple Choice)
4.9/5  (46)
(46)
Find the absolute extrema of the function on the region bounded by the disk defined by .
(Short Answer)
5.0/5  (36)
(36)
Find and classify the relative extrema and saddle points of the function .
(Short Answer)
4.8/5  (43)
(43)
A contour map for a function f is shown. Use it to estimate the value of . 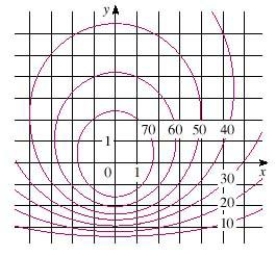
(Multiple Choice)
4.8/5  (39)
(39)
Use Lagrange multipliers to find the maximum value of the function subject to the given constraints.
(Short Answer)
4.9/5  (41)
(41)
Showing 81 - 100 of 132
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)